электронный научно-технический журнал
ИНЖЕНЕРНЫЙ ВЕСТНИК
Издатель: Общероссийская общественная организация "Академия инженерных наук им. А.М. Прохорова".
Инженерный вестник # 09, сентябрь 2012
УДК 517.947.44
Россия, МГТУ им. Н.Э. Баумана
При анализе динамики механических систем часто возникает необходимость учета влияния вариаций параметров системы на ее фазовые координаты, о чём подробно изложено в [1]. Например, при анализе точности системы, когда её параметры имеют допусковый разброс, который носит случайный характер. Наиболее удобным подходом к решению поставленной задачи было бы получение явной аналитической зависимости выходных координат от интересующих нас параметров. При оценке точности линейных нестационарных систем получить такую зависимость, как правило, не удается. Поэтому чтобы получить ее, необходимо разложить фазовые координаты системы в ряд по вариациям параметров с центром разложения, соответствующим номинальным значениям параметров.
Нахождение коэффициентов вышеуказанного ряда связано с вычислением частных производных различного порядка от фазовых координат по параметрам системы. Хотя эта операция хорошо разработана и принципиальных трудностей не вызывает, при высоком порядке исходной системы и большом числе параметров она оказывается весьма громоздкой, а алгоритм для численной реализации - не универсальным. В настоящей работе предлагается метод вычисления коэффициентов разложения, не требующий нахождения частных производных в явном виде и легко реализуемый в виде универсального машинного алгоритма.
Будем считать, что динамика системы описывается векторным дифференциальным уравнением вида
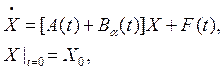 (1)
(1)
где ![]() -
- ![]() -мерный вектор-столбец фазовых координат;
-мерный вектор-столбец фазовых координат; ![]() - квадратная матрица номинальных значений коэффициентов;
- квадратная матрица номинальных значений коэффициентов; ![]() - матрица отклонений коэффициентов уравнения от номинальных значений;
- матрица отклонений коэффициентов уравнения от номинальных значений; ![]() - заданные функции времени, интегрируемые по Риману;
- заданные функции времени, интегрируемые по Риману; ![]() ;
; ![]() - вектор аддитивных возмущений.
- вектор аддитивных возмущений.
Согласно [1] общее решение уравнения (1) можно записать в виде формулы
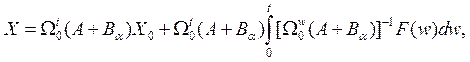 (2)
(2)
где ![]() - нормированная интегральная матрица системы, называемая матрицантом (квадратная матрица, столбцами которой являются
- нормированная интегральная матрица системы, называемая матрицантом (квадратная матрица, столбцами которой являются ![]() линейно независимых решений системы; условие нормировки: при
линейно независимых решений системы; условие нормировки: при ![]() ).
).
Преобразуем прямой и обратный матрицанты, входящие в (2), по известным формулам [2]:
![]() (3)
(3)
![]() (4)
(4)
где ![]() (5)
(5)
В дальнейшем матрицу![]() будем называть матрицей вариаций. В [2], [3] показано, что матрицанты, как прямой так и обратный, от любой матрицы, имеющей интегрируемые по Римману элементы (нестационарные параметры), представимы в виде рядов, которые абсолютно и равномерно сходятся в любой замкнутой части интервала изменения аргумента. Разложим в такие ряды матрицанты от матрицы вариаций, входящие в (3) и (4):
будем называть матрицей вариаций. В [2], [3] показано, что матрицанты, как прямой так и обратный, от любой матрицы, имеющей интегрируемые по Римману элементы (нестационарные параметры), представимы в виде рядов, которые абсолютно и равномерно сходятся в любой замкнутой части интервала изменения аргумента. Разложим в такие ряды матрицанты от матрицы вариаций, входящие в (3) и (4):
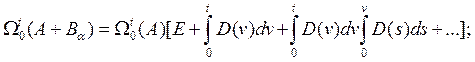 (6)
(6)
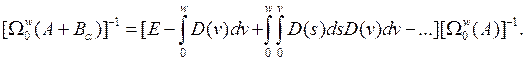 (7)
(7)
Выражение (6) определяет, по существу, разложение общего решения однородного уравнения в ряд по матрице вариаций; получим аналогичное разложение для частного решения. Подставив (6) и (7) во второй член равенства (2), сгруппировав члены с одинаковыми степенями матрицы вариаций и взяв в каждой группе членов некоторые интегралы по частям, запишем частное решение в виде
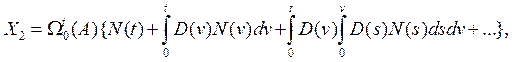 (8)
(8)
где 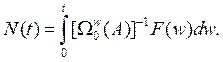
Используя (6) и (8), получим окончательно общее решение неоднородного уравнения (1) в виде ряда по матрице вариаций
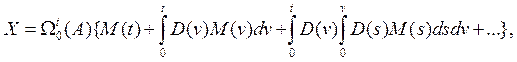 (9)
(9)
где ![]()
Заметим, что каждый последующий член разложения, стоящий в фигурных скобках равенства (9), строится путем умножения предыдущего члена слева на матрицувариаций и интегрирования полученного произведения в заданном интервале изменения аргументаt.
Найдем теперь весовую функцию исследуемой системы относительного![]() -го входа. Для этого рассмотрим реакцию системы управления на воздействие в виде дельта-функции Дирака -
-го входа. Для этого рассмотрим реакцию системы управления на воздействие в виде дельта-функции Дирака - ![]() , приложенного к
, приложенного к ![]() -му входу, т. е.
-му входу, т. е.
![]() (10)
(10)
Подставив (10) в (8) и использовав основное свойство дельта-функции, получим весовую функцию в виде
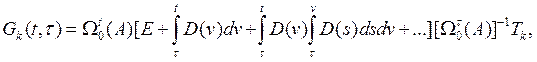 (11)
(11)
где ![]() - вектор-столбец;
- вектор-столбец; ![]() - символ Кронекера.
- символ Кронекера.
Структурно окончательные выражения (8), (9), (11) построены следующим образом. Первый член представляет собой решение для случая номинальных значений коэффициентов уравнения, когда их вариации равны пулю ![]() . Второй член включает в себя матрицувариаций в первой степени. Следовательно, учет только первых двух членов матричного ряда приводит к линеаризации зависимости фазовых координат системы от вариаций параметров, т. е. к принципам теории чувствительности. Остальные члены разложения с более высокими степенями матрицы вариаций последовательно уточняют решение и играют существенную роль только в случае значительных по абсолютной величине вариаций коэффициентов.
. Второй член включает в себя матрицувариаций в первой степени. Следовательно, учет только первых двух членов матричного ряда приводит к линеаризации зависимости фазовых координат системы от вариаций параметров, т. е. к принципам теории чувствительности. Остальные члены разложения с более высокими степенями матрицы вариаций последовательно уточняют решение и играют существенную роль только в случае значительных по абсолютной величине вариаций коэффициентов.
Как правило, при решении инженерных задач анализа САУ нас интересует явное разложение вектора фазовых координат по вариациям, а не формальные соотношения относительно матрицы вариаций. Переход к и нтересующим нас равенствам осуществим, разложив матрицу![]() по матричным единицам. Матричной единицей называется матрица
по матричным единицам. Матричной единицей называется матрица![]() ,у которой элемент с номером
,у которой элемент с номером![]() равен единице, а остальные элементы равны нулю.
равен единице, а остальные элементы равны нулю.
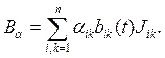 (12)
(12)
Подставив (12) в выражение (5), получим
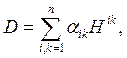 (13)
(13)
где ![]() - квадратная матрица коэффициентов при вариации с номером
- квадратная матрица коэффициентов при вариации с номером ![]() .
.
Теперь, чтобы преобразовать, например, второй член разложения, который согласно (9) можно записать в виде
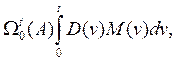 (14)
(14)
подставим в него (13). Проделав несложные преобразования, запишем выражение (14) в виде
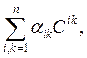 (15)
(15)
где 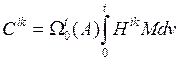 - вектор коэффициентов при вариации с номером
- вектор коэффициентов при вариации с номером ![]() .
.
Подставляя (13) и (15) в третий член равенства (9), можно аналогичным образом получить явное выражение относительно квадратов вариации и т.д.
Таким образом, например, для ![]() -й фазовой координаты (
-й фазовой координаты (![]() -й компоненты вектора) можно записать
-й компоненты вектора) можно записать
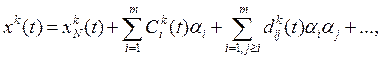 (16)
(16)
где ![]() - число вариаций параметров, которые необходимо учесть при решении конкретной задачи (число вариаций не равных нулю из всех
- число вариаций параметров, которые необходимо учесть при решении конкретной задачи (число вариаций не равных нулю из всех ![]() );
); ![]() - номинальное решение;
- номинальное решение; ![]() - коэффициенты при соответствующих степенях вариаций.
- коэффициенты при соответствующих степенях вариаций.
Коэффициенты уравнения (1) могут быть функциями (в общем случае нелинейными) конструктивных параметров системы. Для того чтобы получить зависимости, аналогичные (16), но относительно вариаций этих параметров, необходимо разложить вышеупомянутые функции в степенные ряды по вариациям, подставить полученные разложения в (16) и перегруппировать члены.
Разобьем основной интервал ![]() на n достаточно малых частей, введя промежуточные точки
на n достаточно малых частей, введя промежуточные точки ![]() и положив
и положив ![]() Выберем на интервале
Выберем на интервале ![]() промежуточную точку
промежуточную точку ![]() (
(![]() ). Тогда прямой и обратный матрицанты вычисляются по формулам [2,3]
). Тогда прямой и обратный матрицанты вычисляются по формулам [2,3]
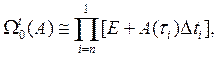 (17)
(17)
 (18)
(18)
Таким образом, расчет по формулам (9) и (11), а также трансформация векторных равенств укладываются в рамки обычных матричных операций и представляют собой, по существу, почти готовый для практической реализации алгоритм.
Результаты работы представляют интерес для параметрического анализа механических систем, где используется теория чувствительности. Методика позволяет определить влияние вариаций параметров объекта, внешних воздействий и условий эксплуатации на динамические характеристики (перемещения, скорости, ускорения) объекта и внутренние силовые факторы в конструкции. Методика использовалась для выбора оптимальных параметров амортизации транспортно-пускового контейнера с летательным аппаратом, размещенного на многоосном шасси высокой проходимости.
Работа поддержана грантом РФФИ №11-08-00699.
ЛИТЕРАТУРА
1. Светлицкий В. А. Статистическая механика и теория надежности: учебник для вузов - М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. – 503 с.
2. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967. – 575 с.
3. Беллман Р. Введение в теорию матриц. М.: Наука, 1969. – 367 с.
Публикации с ключевыми словами: параметры механической системы, фазовые координаты, фундаментальная матрица, функции чувствительности
Публикации со словами: параметры механической системы, фазовые координаты, фундаментальная матрица, функции чувствительности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (499) 263-69-71 |
|
||||
| © 2003-2024 «Инженерный вестник» Тел.: +7 (499) 263-69-71 | |||||



