электронный научно-технический журнал
ИНЖЕНЕРНЫЙ ВЕСТНИК
Издатель: Общероссийская общественная организация "Академия инженерных наук им. А.М. Прохорова".
Инженерный вестник # 10, октябрь 2012
УДК 629.7.017
Россия, МГТУ им. Н.Э. Баумана
Излагается метод, основанный на представлении фазовых координат системы в виде ряда по случайным вариациям параметров. Строится инженерная методика для определения либо границ области, в которую попадают с заданной вероятностью реализации исследуемой фазовой координаты, либо вероятности попадания этой координаты в заданный допуск. Разработан способ выявления влияния разброса каждого в отдельности параметра на динамическую ошибку системы.
Рассмотрим механическую систему, описываемую векторным дифференциальным уравнением
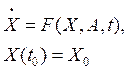 (1)
(1)
где ![]() - n-мерный вектор фазовых координат;
- n-мерный вектор фазовых координат; ![]() - n-мерная векторная функция;
- n-мерная векторная функция; ![]() - вектор случайных параметров;
- вектор случайных параметров; ![]() - время.
- время.
Задача может формулироваться двояко: определение границ области, в которую с заданной вероятностью попадают реализации исследуемой фазовой координаты или вычисление вероятности попадания реализаций в заданный допуск.
Распространенным подходом к решению такого рода задач является разложение фазовых координат в степенной ряд по случайным вариациям с центром разложения, соответствующим номинальным значениям параметров. Для случая нелинейных систем можно воспользоваться известными приемами теории чувствительности [1].
Будем считать, что такое разложение получено. Тогда путем осреднения как самих фазовых координат (или ошибок ![]() , где
, где ![]() - номинальное решение), так и их степеней, несложно выразить моменты различных порядков в виде явных зависимостей от вероятностных характеристик параметров системы.
- номинальное решение), так и их степеней, несложно выразить моменты различных порядков в виде явных зависимостей от вероятностных характеристик параметров системы.
Для весьма распространенного на практике случая нормальности закона распределения параметров и их независимости получаются формулы полиномиального вида от дисперсии. Например, для математического ожидания ошибки имеем
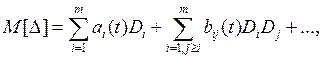 (2)
(2)
где ![]() - количество параметров, допусковый разброс которых необходимо учесть при анализе точности;
- количество параметров, допусковый разброс которых необходимо учесть при анализе точности; ![]() - дисперсии параметров. Вычисление коэффициентов
- дисперсии параметров. Вычисление коэффициентов ![]() и т.д. принципиальных сложностей не имеет.
и т.д. принципиальных сложностей не имеет.
В дальнейшем ограничиваемся определением четырех характеристик - ![]() (
(![]() - математическое ожидание;
- математическое ожидание; ![]() - дисперсия;
- дисперсия; 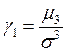 - асимметрия;
- асимметрия; 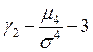 - эксцесс).
- эксцесс).
Для практических задач, рассмотренных в [2], важно получить границы области, в которую с заданной вероятностью попадают реализации исследуемой фазовой координаты. Задача в такой постановке достаточно просто решается только в случае нормального закона распределения, когда удается в долях среднего квадратического отклонения задать координаты границ такой области (например, правило «![]() » обеспечивает вероятность 0,9973). Для произвольного закона распределения решение поставленной задачи в современных публикациях отсутствует.
» обеспечивает вероятность 0,9973). Для произвольного закона распределения решение поставленной задачи в современных публикациях отсутствует.
Получим границы указанной области для законов распределения более общего вида. Для этого используем разложение произвольной функции распределения в ряд Грама-Шарлье [3], ограничиваясь тремя членами. Тогда
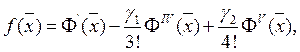 (3)
(3)
где ![]() - нормальная функция распределения,
- нормальная функция распределения,  - безразмерная координата.
- безразмерная координата.
Добьемся того, чтобы интеграл от (3) в пределах ![]() обеспечивал вероятность
обеспечивал вероятность![]() попадания в интервал
попадания в интервал ![]() . Тогда
. Тогда
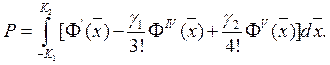 (4)
(4)
Таким образом, получено уравнение для нахождения границ области ![]() , в котором, в зависимости от конкретных условий, можно задать любое численное значение вероятности
, в котором, в зависимости от конкретных условий, можно задать любое численное значение вероятности ![]() . Рассмотрим, например,
. Рассмотрим, например, ![]() = 0,9973, т. е. то же самое значение вероятности, что и для правила «
= 0,9973, т. е. то же самое значение вероятности, что и для правила «![]() » в случае нормального закона распределения.
» в случае нормального закона распределения.
Для того чтобы определение![]() и
и![]() из (4) стало корректным, необходимо наложить еще одно условие па границы области. Из практических соображений целесообразно вычислять
из (4) стало корректным, необходимо наложить еще одно условие па границы области. Из практических соображений целесообразно вычислять![]() при условии — минимумаинтервала
при условии — минимумаинтервала![]() . Для удовлетворения этого требования использовался следующий алгоритм, реализованный на ЭВМ. Интервал интегрирования функции плотности вероятности (3) разбивался на равные элементарные участки. Суммирование осуществлялось последовательно по шагам, причем на каждом шаге выбиралась та элементарная площадка из оставшихся, на которой достигался максимум плотности вероятности. Таким образом, выбирая на каждом шаге элементарную площадку с максимальной площадью, обеспечиваем минимум шагов для достижения заданной суммарной вероятности, что соответствует требованию минимума интервала
. Для удовлетворения этого требования использовался следующий алгоритм, реализованный на ЭВМ. Интервал интегрирования функции плотности вероятности (3) разбивался на равные элементарные участки. Суммирование осуществлялось последовательно по шагам, причем на каждом шаге выбиралась та элементарная площадка из оставшихся, на которой достигался максимум плотности вероятности. Таким образом, выбирая на каждом шаге элементарную площадку с максимальной площадью, обеспечиваем минимум шагов для достижения заданной суммарной вероятности, что соответствует требованию минимума интервала![]() . Процесс суммирования заканчивался, когда общая площадь становилась равной 0,9973.
. Процесс суммирования заканчивался, когда общая площадь становилась равной 0,9973.
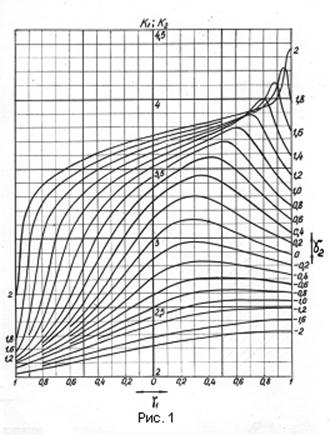
В результате проведенных расчетов была построена номограмма (рис. 1). По вертикальной оси отложены значения ![]() , по горизонтальной — асимметрия. Каждая кривая соответствует определенному значению эксцесса. Номограммой нужно пользоваться, придерживаясь следующего правила. Выбрать из семейства кривую, соответствующую конкретному
, по горизонтальной — асимметрия. Каждая кривая соответствует определенному значению эксцесса. Номограммой нужно пользоваться, придерживаясь следующего правила. Выбрать из семейства кривую, соответствующую конкретному![]() . Если
. Если ![]() , то справа от вертикальной оси при пересечении выбранной кривой с координатной линией, соответствующей
, то справа от вертикальной оси при пересечении выбранной кривой с координатной линией, соответствующей ![]() , получим
, получим![]() , слева от оси для того же
, слева от оси для того же ![]() получим
получим ![]() . Для случая
. Для случая ![]() границы меняются местами.
границы меняются местами.
Определив ![]() и
и![]() и приняв за начало отсчета номинальное решение, запишем верхнюю и нижнюю границы области в любой момент времени в виде
и приняв за начало отсчета номинальное решение, запишем верхнюю и нижнюю границы области в любой момент времени в виде
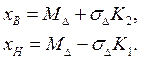 (5)
(5)
Из рис. 1 видно, что правило «![]() » получается как частный случай при
» получается как частный случай при ![]() , что соответствует нормальному закону распределения.
, что соответствует нормальному закону распределения.
Очевидно, что при очень сильном отличии закона распределения от нормального (большие по абсолютной величине ![]() и
и ![]() ) предлагаемая методика окажется непригодной, поскольку потребуется учет большего числа членов ряда Грама-Шарлье, а следовательно, и вычисление более высоких моментов. Принятые для данной номограммы пределы изменения
) предлагаемая методика окажется непригодной, поскольку потребуется учет большего числа членов ряда Грама-Шарлье, а следовательно, и вычисление более высоких моментов. Принятые для данной номограммы пределы изменения ![]() и
и ![]() (
(![]() ) проверялись на конкретных законах распределения, имеющих точную аналитическую запись. При этом ошибка определения границ области с помощью номограммы по отношению к точно вычисленным границам не превышала 5 %.
) проверялись на конкретных законах распределения, имеющих точную аналитическую запись. При этом ошибка определения границ области с помощью номограммы по отношению к точно вычисленным границам не превышала 5 %.
Выясним теперь, как влияет разброс каждого в отдельности параметра на динамическую ошибку системы (на границы найденной выше области). Для этого вычислим частные производные от функций границ области по средним квадратическим отклонениям вариаций параметров в точке заданных значений этих средних квадратических отклонений. Абсолютные величины производных определят «вес» каждой вариации и тем самым дадут возможность выявить их «иерархию».
Продифференцировав (5), получим
 (6)
(6)
Считая ![]() и
и ![]() сложными функциями от
сложными функциями от ![]() , можно записать
, можно записать
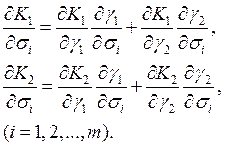 (7)
(7)
Все элементы формул (6), (7) легко вычисляются на компьютере в конечных разностях, при этом 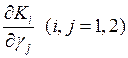 целесообразно табулировать для различных значений
целесообразно табулировать для различных значений ![]() и
и ![]() .
.
Для сравнительного анализа могут оказаться более удобными «весовые» коэффициенты ![]() , например, для верхней границы имеющие вид
, например, для верхней границы имеющие вид
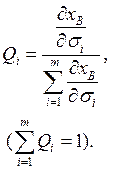 (8)
(8)
Таким образом, прямую задачу можно считать решенной. Обратная задача -определение вероятности попадания реализаций фазовой координаты в заданный допуск - решается достаточно просто путем интегрирования выражения (3) в пределах, соответствующих допуску. Необходимые в этом случае таблицы производных от нормальной функции распределения можно найти в [3], либо использовать возможности математических прикладных программ, например, Matlab, Mathematica, Mathcad, Statistica.
На основании представленной инженерной методики были проведены исследования надёжности системы амортизации транспортного средства. В состав упруго-массовой расчетной модели входило более пятидесяти параметров, допусковый случайный разброс которых учитывался при определении максимальных значений перемещений и скоростей штоков амортизаторов.
Работа поддержана грантом РФФИ № 11-08-00699.
ЛИТЕРАТУРА
1. Розенвассер Е.Н., Юсупов Р.М. Методы теории чувствительности в автоматическом управлении Л: Энергия, Ленинградское отделение, 1971. – 344 с.
2. Светлицкий В. А. Статистическая механика и теория надежности: учебник для вузов - М. : Изд-во МГТУ им. Н. Э. Баумана, 2002. – 503 с.
3. Крамер Г. Математические методы статистики. М.: Мир, 1979. – 648 с.
Публикации с ключевыми словами: параметры механической системы, фазовые координаты, случайная величина, вероятность попадания реализации в заданный допуск
Публикации со словами: параметры механической системы, фазовые координаты, случайная величина, вероятность попадания реализации в заданный допуск
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (499) 263-69-71 |
|
||||
| © 2003-2024 «Инженерный вестник» Тел.: +7 (499) 263-69-71 | |||||



