научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0587745
УДК 519.85
Россия, МГТУ им. Н.Э. Баумана
1. ВВЕДЕНИЕ
Поиск ситуации равновесия по Нэшу матричной игры в смешанных стратегиях игроков обычно проводится методом полного перебора [1, 2], вообще говоря, не приемлемого для практического применения. Этот подход имеет экспоненциальную сложность вычислений: нужно решить ![]() систем линейных уравнений и неравенств, где m – общее число чистых стратегий всех участников игры. В работе предложен и апробирован игровой алгоритм, который, предполагается, имеет полиномиальную сложность.
систем линейных уравнений и неравенств, где m – общее число чистых стратегий всех участников игры. В работе предложен и апробирован игровой алгоритм, который, предполагается, имеет полиномиальную сложность.
В бескоалиционной матричной игре nлиц каждый игрок k=1,2,…,n располагает конечным множеством чистых стратегий ![]() . Игра полностью определяется заданием функций выигрыша игроков, которые будем представлять ковариантными тензорами n-го ранга
. Игра полностью определяется заданием функций выигрыша игроков, которые будем представлять ковариантными тензорами n-го ранга ![]() . (Координаты тензора
. (Координаты тензора ![]() равны величинам выигрышей k-го игрока в зависимости от выбора всеми игроками своих чистых стратегий
равны величинам выигрышей k-го игрока в зависимости от выбора всеми игроками своих чистых стратегий ![]() .)
.)
Рассматривается смешанное расширение игры, в котором всегда существует равновесие по Нэшу (см. [1, 2]). Именно, каждый игрок применяет смешанную стратегию, т.е. выбирает случайную величину, принимающую значения в его множестве чистых стратегий. Смешанные стратегии будем отождествлять с вероятностными распределениями ![]() . С вероятностью
. С вероятностью ![]() игрок kвыбирает свою i-ю,
игрок kвыбирает свою i-ю, ![]() , чистую стратегию. По смыслу, векторы
, чистую стратегию. По смыслу, векторы ![]() (контравариантные тензоры первого ранга) принадлежат симплексам
(контравариантные тензоры первого ранга) принадлежат симплексам 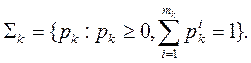
В принятых обозначениях средние выигрыши игроков, которые они стремятся, по возможности, увеличить, могут быть записаны как тензорные произведения
![]()
В соответствии с обычными соглашениями в выражениях (1) опущен знак суммирования, которое проводится по совпадающим верхним и нижним индексам.
Напомним (см. [1],[2]), что ситуацией равновесия по Нэшу, называется набор стратегий игроков ![]() , удовлетворяющий условию
, удовлетворяющий условию ![]() , в котором, для упрощения записи, выражение (1) обозначено как
, в котором, для упрощения записи, выражение (1) обозначено как ![]() , а
, а ![]() - то же тензорное произведение, что и (1), p═p*, в котором вместо сомножителя
- то же тензорное произведение, что и (1), p═p*, в котором вместо сомножителя ![]() взято
взято ![]() .
.
Цель работы – построение игрового алгоритма поиска одного из равновесий по Нэшу. Под этим понимается приводящая к равновесию многошаговая вычислительная схема, моделирующая процесс игры как поочередный выбор ее участниками своих стратегий.
2. МЕТОД ПОИСКА РАВНОВЕСИЯ
Поиск равновесия игры сведем к решению следующей многоэкстремальной задачи математического программирования. Требуется найти глобальный максимум целевой функции
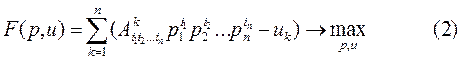
по переменным p,u, ![]() , удовлетворяющим ограничениям
, удовлетворяющим ограничениям
![]()
В левой части неравенств (3) ![]() - тензорное произведение (1), из которого исключен k-й сомножитель
- тензорное произведение (1), из которого исключен k-й сомножитель ![]() , а
, а ![]() - ковариантный тензор первого ранга размерности
- ковариантный тензор первого ранга размерности ![]() с координатами, равными единице.
с координатами, равными единице.
Очевидна следующая
Теорема 1. Глобальный максимум целевой функции (2) на множестве (3), имеющий значение, равное нулю, достигается лишь в точках (p*,u*), отвечающих ситуациям равновесия игры p*, в которых координаты вектора u* - величины средних выигрышей игроков.
Соотношения (2),(3) дают основание для рассмотрения следующей игры nлиц, в которой участники k=1,2,…,nпри выборе своих стратегий ![]() (вектор
(вектор ![]() получен из uисключением k-й координаты) “руководствуются” целевыми функциями (ср. с (2)):
получен из uисключением k-й координаты) “руководствуются” целевыми функциями (ср. с (2)):
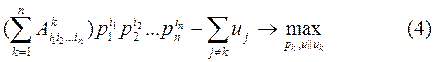
при ограничениях
![]()
При любых фиксированных стратегиях партнеров каждая из функций выигрыша (4) является линейной по переменной ![]() , представляющей стратегию, выбираемую k-м игроком. Таким образом, имеем набор (4, 5), k=1,2,…,n, взаимосвязанных задач линейного программирования (ЛП). Можно также считать (и это делается в дальнейшем), что стратегиями игроков являются лишь векторы
, представляющей стратегию, выбираемую k-м игроком. Таким образом, имеем набор (4, 5), k=1,2,…,n, взаимосвязанных задач линейного программирования (ЛП). Можно также считать (и это делается в дальнейшем), что стратегиями игроков являются лишь векторы ![]() В самом деле, ситуация игры p однозначно определяет вектор u. Поэтому бескоалиционная игра (4, 5), k=1,2,…,n, как и исходная игра, также является матричной.
В самом деле, ситуация игры p однозначно определяет вектор u. Поэтому бескоалиционная игра (4, 5), k=1,2,…,n, как и исходная игра, также является матричной.
Замечание 1. При n=2 и ![]() имеем антагонистическую игру, для которой задачи ЛП (4),(5) взаимно двойственны [3]. Их решение
имеем антагонистическую игру, для которой задачи ЛП (4),(5) взаимно двойственны [3]. Их решение ![]() дает искомую ситуацию равновесия (см. [1-3]).
дает искомую ситуацию равновесия (см. [1-3]).
Замечание 2. Всякая ситуация равновесия (p′,v′) в игре (4, 5) дает точку максимума функции (2), ![]() по каждой из переменных
по каждой из переменных ![]() при фиксированных значениях остальных переменных.
при фиксированных значениях остальных переменных.
Ввиду замечания 2 равновесия по Нэшу в игре (4, 5) будем называть стационарными точками целевой функции F (см. (2)).
Игра (4, 5) намного проще исходной задачи. В ней игроки приходят к равновесию, поочередно делая свои “ходы” (т.е. выбирая свои стратегии на шагах t═0,1,…), начиная игру из произвольной начальной ситуации p(0):
Теорема 2. Пусть игроки k═1,2,…,n поочередно, на шагах t=0,1,…, изменяют свои стратегии так, чтобы ![]() было решением задачи ЛП (4),(5), k═1,2,…,n, в которой фиксированы все векторы,
было решением задачи ЛП (4),(5), k═1,2,…,n, в которой фиксированы все векторы, ![]() а
а![]() . Тогда
. Тогда ![]() где
где ![]() - некоторая ситуация равновесия в игре (4, 5).
- некоторая ситуация равновесия в игре (4, 5).
Доказательство.Значения целевой функции (2), ![]() , по построению образуют монотонно возрастающую, а, следовательно, сходящуюся последовательность. Ввиду компактности множеств смешанных стратегий игроков можно считать, что последовательность
, по построению образуют монотонно возрастающую, а, следовательно, сходящуюся последовательность. Ввиду компактности множеств смешанных стратегий игроков можно считать, что последовательность ![]() также сходится к некоторому вектору
также сходится к некоторому вектору ![]() (см. подобные рассуждения в [4]). Предельный переход в ограничениях и целевых функциях задач ЛП (4),(5) показывает, что координаты
(см. подобные рассуждения в [4]). Предельный переход в ограничениях и целевых функциях задач ЛП (4),(5) показывает, что координаты ![]() вектора
вектора ![]() служат решениями всех этих задач, а
служат решениями всех этих задач, а ![]() является равновесием игры (4),(5).
является равновесием игры (4),(5).
Через ![]() обозначим двойственные переменные, с помощью которых снимаются ограничения в форме неравенств (3) при решении экстремальной задачи (2),(3) методом множителей Лагранжа. Введем функцию Лагранжа, которая, по определению, имеет вид (см. [5])
обозначим двойственные переменные, с помощью которых снимаются ограничения в форме неравенств (3) при решении экстремальной задачи (2),(3) методом множителей Лагранжа. Введем функцию Лагранжа, которая, по определению, имеет вид (см. [5])
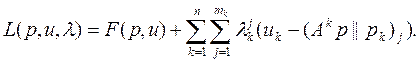
Рассмотрим также множители Лагранжа, ![]() - двойственные переменные в задачах ЛП (4),(5), k=1,2,…,n. Анализ двойственных к (4),(5) задач ЛП (см. [3]) показывает, что переменные
- двойственные переменные в задачах ЛП (4),(5), k=1,2,…,n. Анализ двойственных к (4),(5) задач ЛП (см. [3]) показывает, что переменные ![]() удовлетворяют ограничениям
удовлетворяют ограничениям ![]() Необходимые условия экстремума в задаче (2),(3) также приводят к ограничению
Необходимые условия экстремума в задаче (2),(3) также приводят к ограничению ![]()
Далее для упрощения записи будем опускать переменные u,vи упоминать лишь о переменной p, говоря об оптимизации функции (2) на множестве (3) или об игре (4),(5). Пусть p* является стационарной точкой функции (2), а ![]() - соответствующие векторыдвойственных переменных в задачах (2, 3) и (4, 5), p=p*, k=1,2,…,n, соответственно.
- соответствующие векторыдвойственных переменных в задачах (2, 3) и (4, 5), p=p*, k=1,2,…,n, соответственно.
Замечание 3. Имеют место равенства ![]()
Согласно замечанию 2 итерационный процесс из теоремы 2, сходясь к стационарной точке функции F, вообще говоря, не дает решения исходной игры. Для выхода из областей притяжения стационарных точек функции (2) с целью нахождения глобального максимума (см. теорему 1) будем использовать следующее свойство экстремальной задачи (2, 3).
Теорема 3. Стационарная точка p=p* целевой функции (2) является равновесием по Нэшу в исходной игровой задаче тогда и только тогда, когда найдутся такие множители Лагранжа, что ![]()
Доказательство. Достаточность указанного условия следует из теоремы 1 ввиду того, что ![]() и
и ![]()
Пусть теперь p* является равновесием по Нэшу. Тогда выполняются условия дополняющей нежесткости (см. [1]-[3]) с множителями p*:
![]()
которым удовлетворяют и множители Лагранжа ![]() . Отсюда следует, что функция Лагранжа
. Отсюда следует, что функция Лагранжа ![]() (ввиду
(ввиду ![]() по замечанию 3) , построенная для задачи ЛП (4, 5),
по замечанию 3) , построенная для задачи ЛП (4, 5), ![]() имеет минимум
имеет минимум ![]() по двойственной переменной. Более того, взяв
по двойственной переменной. Более того, взяв ![]() получим (сумма
получим (сумма 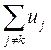 сокращается):
сокращается):
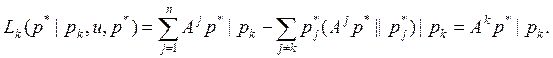
По определению ситуации равновесия, точка ![]() является максимумом функции
является максимумом функции ![]() на множестве
на множестве ![]() . Таким образом (см. [4, с. 219]), пара
. Таким образом (см. [4, с. 219]), пара ![]() является седловой точкой функции Лагранжа
является седловой точкой функции Лагранжа ![]() по переменным
по переменным ![]() . Следовательно, векторы
. Следовательно, векторы ![]() являются множителями Лагранжа. Проведенные рассуждения справедливы при любом k=1,2,…,n. Теорема доказана.
являются множителями Лагранжа. Проведенные рассуждения справедливы при любом k=1,2,…,n. Теорема доказана.
Замечание 4. В достаточном условии теоремы 3 можно потребовать выполнение условия ![]() лишь для одного из игроков k=1,2,…,n.
лишь для одного из игроков k=1,2,…,n.
3. АЛГОРИТМ ПОИСКА РАВНОВЕСИЯ
В соответствии с теоремами 1-3 и замечаниями 3, 4 предлагается использовать следующую многошаговую схему поиска равновесия.
Этап 0. Задать произвольно начальную ситуацию игры ![]() .
.
Этап 1. Каждому участнику игры (4),(5) поочередно, в порядке нумерации, выбрать свою оптимальную (в текущей ситуации) стратегию и сообщить ее партнерам. По достижении некоторой ситуации равновесия ![]() проверить выполнение условия
проверить выполнение условия ![]() . Если это так, то СТОП. Иначе перейти к выполнению этапа 2.
. Если это так, то СТОП. Иначе перейти к выполнению этапа 2.
Этап 2. Найти номер sодного из игроков, для которого имеется наибольшее число совпадающих векторов прямых![]() и двойственных
и двойственных ![]() переменных. Игроку sприменить стратегию, оптимальную в ситуации
переменных. Игроку sприменить стратегию, оптимальную в ситуации ![]() , и сообщить ее всем остальным участникам игры. Перейти к этапу 1.
, и сообщить ее всем остальным участникам игры. Перейти к этапу 1.
Поясним сказанное. На этапе 1 разворачивается итерационный процесс, рассмотренный в теореме 2. По теореме 3 выполнение проверяемого условия означает достижимость одной из искомых ситуаций равновесия по Нэшу в исходной игре. Вычисления оптимальных стратегий игроков и отвечающих им двойственных переменных будем проводить с помощью симплекс-метода (см. [3]).
Вычислительный эксперимент.Пусть n═3, ![]() Для записи функции выигрыша любого, k-го игрока, использована матрица платежей, номера строк iи столбцов jкоторой совпадают с номерами чистых стратегий игроков
Для записи функции выигрыша любого, k-го игрока, использована матрица платежей, номера строк iи столбцов jкоторой совпадают с номерами чистых стратегий игроков ![]() соответственно
соответственно ![]() Элемент i,jэтой матрицы представляет собой строку чисел, равных выигрышам k-го игрока в зависимости от выбора им чистых стратегий
Элемент i,jэтой матрицы представляет собой строку чисел, равных выигрышам k-го игрока в зависимости от выбора им чистых стратегий ![]() соответственно. Итак, пусть платежные матрицы игроков k=1,2,…,nимеют вид
соответственно. Итак, пусть платежные матрицы игроков k=1,2,…,nимеют вид
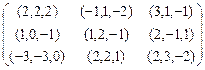 ,
,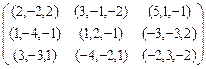 ,
,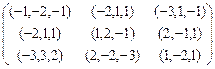 .
.
Например, игрок 1 получает платежи 2,-1,1 в ситуациях (1,2,3), (2,2,3), (3,2,3) соответственно, т.е. при условии, что остальные участники игры ![]() применяют стратегии
применяют стратегии ![]()
Возьмем начальную ситуацию ![]() На этапе 1 получаем стационарную точку
На этапе 1 получаем стационарную точку ![]() :
:

(Значение целевой функции F=−0.27.) На этапе 2 игрок s=2 имеет стратегию(0.67,0.33,0), оптимальную в ситуации ![]() .
.
Последующие вычисления этапа 1 дают новую стационарную точку ![]() :
:
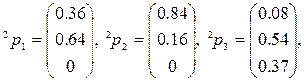
в которой F=−0.2. Двойственные переменные равны
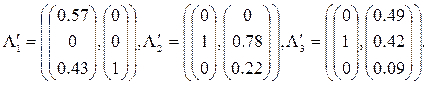
Вновь выбирая игрока s=2, найдем его стратегию (0,1,0), оптимальную в ситуации ![]() .
.
Выполнив вычисления этапа 1, найдем очередную стационарную точку ![]() и отвечающие ей двойственные переменные (при этом F=−0.19):
и отвечающие ей двойственные переменные (при этом F=−0.19):
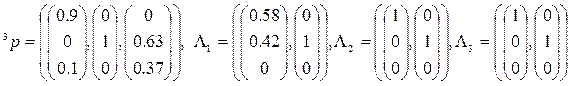
На этапе 2 берем теперь s=3, так как только у третьего игрока имеются совпадающие векторы прямых и двойственных переменных: ![]() . Оптимальная для ситуации
. Оптимальная для ситуации ![]() стратегия игрока 3 равна (0,0,1).
стратегия игрока 3 равна (0,0,1).
Следуя предложенной схеме, последовательно находим стационарные точки (со значениями F=−0.004 и F=−0.12 соответственно)
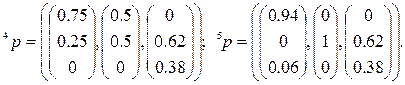
На этапе 2, в ситуации ![]() , было выбрано s=2, а в ситуации
, было выбрано s=2, а в ситуации ![]() - s=3. В результате получаем искомое равновесие
- s=3. В результате получаем искомое равновесие ![]() :
:

Всего в процессе работы алгоритма было решено около двадцати задач ЛП, в которых текущие ситуации каждый раз использовались в качестве начальных приближений.
Заключение. Задачи ЛП имеют полиномиальную сложность решения (см. [6]). Это дает основание предположить, что предложенный в работе алгоритм имеет такую же вычислительную сложность.
СПИСОК ЛИТЕРАТУРЫ
1. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. М.: Высшая школа, 1998. 304 с.
2. Васин А.А., Морозов В.В. Теория игр и модели математической экономики. М.: Изд-во МГУ, 2005. 278 с.
3. Ашманов С.А. Линейное программирование. М.: Наука, 1981. 340 с.
4. Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1980. 518 с.
5. Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974. 481 с.
6. Хачиян Л.Г. Полиномиальный алгоритм в линейном программировании //Докл. АН СССР. 1979. Т. 244, № 5. С. 1093-1096.
Публикации с ключевыми словами: тензор, линейное программирование, равновесие по Нэшу, матричная игра, смешанные стратегии, теория двойственности, множители Лагранжа, глобальный максимум, тензорное произведение
Публикации со словами: тензор, линейное программирование, равновесие по Нэшу, матричная игра, смешанные стратегии, теория двойственности, множители Лагранжа, глобальный максимум, тензорное произведение
Смотри также:
- Повышение быстродействия задачи конфликтно-оптимального целераспределения малых групп летательных аппаратов
- Алгоритмы распределения ресурсов для защиты информации между объектами информационной системы на основе игровой модели и принципа равной защищенности объектов
- Минимизация неизбежных потерь материалов в промышленном производстве при их раскрое на штучные заготовки
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



