электронный научно-технический журнал
ИНЖЕНЕРНЫЙ ВЕСТНИК
Издатель: Общероссийская общественная организация "Академия инженерных наук им. А.М. Прохорова".
Инженерный вестник # 05, май 2012
УДК 621.378:551.508
Россия, МГТУ им. Н.Э. Баумана
Лазерные методы являются наиболее перспективными для оперативного локального газоанализа (см., например, [1-6]). Если качественный состав газовой смеси известен, то измерение концентраций газов может быть проведено путем регистрации поглощения газовой смеси для определенного набора спектральных каналов измерения.
Задача нахождения концентраций газов из результатов многоспектральных (например, лазерных оптико-акустических) измерений для узкополосного лазерного источника обычно сводится к решению системы линейных алгебраических уравнений вида [3, 4] (считаем, что смесь содержит М/2 газовых компонент, измерения проводятся на М длинах волн, а ширина линий генерации лазера много меньше ширины линий поглощения газов):
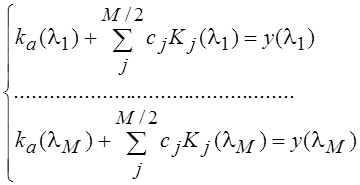 , (1)
, (1)
где:
![]() приведенный измеряемый сигнал на длине волны
приведенный измеряемый сигнал на длине волны ![]() (например, для лазерного оптико-акустического газоанализатора
(например, для лазерного оптико-акустического газоанализатора 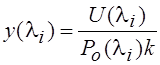 ,
, ![]() - сигнал, измеряемый оптико-акустическим детектором;
- сигнал, измеряемый оптико-акустическим детектором; ![]() - мощность излучения лазера;
- мощность излучения лазера; ![]() - чувствительность оптико-акустического детектора);
- чувствительность оптико-акустического детектора);
![]() показатели неселективного (фонового) поглощения на длине волны
показатели неселективного (фонового) поглощения на длине волны ![]() ;
;
![]() - коэффициент поглощения j-ой газовой компоненты смеси на длине волны
- коэффициент поглощения j-ой газовой компоненты смеси на длине волны ![]() ;
;
![]() - концентрация j-ой газовой компоненты смеси;
- концентрация j-ой газовой компоненты смеси;
М – число спектральных каналов;
K =![]() - полное число газовых компонент в анализируемой смеси.
- полное число газовых компонент в анализируемой смеси.
Неизвестными величинами в системе уравнений (1) являются ![]() и
и ![]() .
.
В матричной форме уравнение (1) имеет следующий вид (см., например, [4]):
![]() , (2)
, (2)
где:
![]() - M-мерный вектор показателей неселективного поглощения;
- M-мерный вектор показателей неселективного поглощения;
![]() - матрица коэффициентов поглощения газов размерностью
- матрица коэффициентов поглощения газов размерностью ![]() ;
;
![]() - M/2-мерный вектор концентраций газов;
- M/2-мерный вектор концентраций газов;
![]() - M-мерный вектор измеряемых сигналов (показателей поглощения исследуемой смеси).
- M-мерный вектор измеряемых сигналов (показателей поглощения исследуемой смеси).
Коэффициенты ![]() слабо зависят от длины волны. Поэтому обычно спектральные каналы измерения выбирают попарно (для каждого газового компонента) достаточно близко, так что для них коэффициенты
слабо зависят от длины волны. Поэтому обычно спектральные каналы измерения выбирают попарно (для каждого газового компонента) достаточно близко, так что для них коэффициенты ![]() можно положить равными константе. В этом случае из М спектральных каналов, необходимых для контроля газовой смеси, информация М/2 каналов требуется для определения концентраций газов, а информация других М/2 каналов - для определения показателей
можно положить равными константе. В этом случае из М спектральных каналов, необходимых для контроля газовой смеси, информация М/2 каналов требуется для определения концентраций газов, а информация других М/2 каналов - для определения показателей ![]() . В этом случае уравнение (2) лазерного газоанализа преобразуется к виду:
. В этом случае уравнение (2) лазерного газоанализа преобразуется к виду:
![]() , (3)
, (3)
где:
![]() - матрица системы (1) размерностью
- матрица системы (1) размерностью ![]() ;
;
![]() - M-мерный искомый вектор (M/2 компонент этого вектора соответствуют концентрациям газов, другие M/2 компонент - показателям неселективного поглощения).
- M-мерный искомый вектор (M/2 компонент этого вектора соответствуют концентрациям газов, другие M/2 компонент - показателям неселективного поглощения).
Решение уравнения (3) имеет вид:
![]() . (4)
. (4)
При реальных измерениях правая часть уравнения (3) всегда известна со случайной ошибкой. Таким образом, в (2) и (3) вместо ![]() имеем:
имеем:
![]() , (5)
, (5)
где:
![]() - М –мерный вектор шума измерения.
- М –мерный вектор шума измерения.
Случайные ошибки данных измерений приводят (при нахождении решения (4)) к вариациям искомых величин. Эти вариации могут быть очень велики при большом числе обусловленности матрицы ![]() .
.
Обычно такая ситуация (большие вариации искомых концентраций газов) возникает при обработке данных спектральных измерений для многокомпонентных смесей с перекрывающимися спектрами поглощения (см., например, [4-6]).
Для малокомпонентных смесей (две, три, четыре газовые компоненты в анализируемой смеси) вариации искомых концентраций газов (при использовании решения (4)) обычно невелики (см. результаты математического моделирования и обработки экспериментальных данных, например, в [4-6]) .
Однако, для сложных малокомпонентных смесей (в которых газовые компоненты при выбранных спектральных каналах измерения имеют гладкий спектр поглощения без выраженных максимумов (пиков) поглощения или концентрации газовых компонент смеси отличаются на несколько порядков) небольшой шум (небольшие малые вариации данных измерений) могут приводить (при попытке использовать решение (4)) к большим вариациям искомых величин.
Выход из этой трудности заключается в использовании специальных алгоритмов обработки, основанных на методах решения некорректных математических задач [7, 8].
Ниже рассматривается метод определения концентраций газов в сложных малокомпонентных смесях, основанный на построении байесовской оценки решения.
Существующие методы построения оценок можно разделить на два класса (см., например, [7]). К первому относятся методы, для которых характерно использование функции потерь. Оценки, полученные этими методами, минимизируют принятую функцию потерь. Второй класс объединяет методы построения оценок, которые максимизируют апостериорную плотность вероятности.
Для задачи лазерного газоанализа трудно задать или отдать предпочтение какой-либо функции потерь. Поэтому оценку решения уравнения лазерного газоанализа будем определять из условия максимума апостериорной плотности вероятности.
Построение байесовской оценки вектора ![]() для уравнения лазерного газоанализа (3) будем проводить при следующих предположениях:
для уравнения лазерного газоанализа (3) будем проводить при следующих предположениях:
1. Вектор шума измерения ![]() подчиняется нормальному распределению, некоррелирован с измеряемым сигналом и имеет нулевое среднее значение и корреляционную матрицу
подчиняется нормальному распределению, некоррелирован с измеряемым сигналом и имеет нулевое среднее значение и корреляционную матрицу ![]() .
.
2. Априорное распределение искомого вектора ![]() также является нормальным с некоторым средним значением
также является нормальным с некоторым средним значением ![]() и корреляционной матрицей
и корреляционной матрицей ![]() .
.
3. Матрицы ![]() и
и ![]() обратимы (существуют матрицы
обратимы (существуют матрицы ![]() и
и ![]() ).
).
При сделанных предположениях показано [7], что апостериорная плотность вероятности является нормальной и байесовская оценка ![]() вектора
вектора ![]() совпадает с оценкой, определяемой из максимума апостериорной плотности вероятности. Таким образом, байесовская оценка
совпадает с оценкой, определяемой из максимума апостериорной плотности вероятности. Таким образом, байесовская оценка ![]() вектора
вектора ![]() определяется следующим выражением [7]:
определяется следующим выражением [7]:
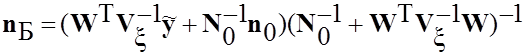 (6)
(6)
Здесь верхний индекс "Т" означает транспонирование матрицы, верхний индекс "-1" – обратную матрицу.
Устойчивость полученного методом байесовской оценки решения достигается сужением класса возможных решений и это сужение основывается на вводимой априорной информации. Такая априорная информация (среднее значение и корреляционная матрица) может быть вполне доступна во многих задачах, например, при рутинном газоанализе.
Для проверки работоспособности метода байесовских оценок в задаче газоанализа сложных смесей проводилось математическое моделирование. Матрицы ![]() и
и ![]() задавались в виде диагональных матриц [7] с элементами по диагонали равными дисперсиям шума измерения в спектральных каналах (для матрицы
задавались в виде диагональных матриц [7] с элементами по диагонали равными дисперсиям шума измерения в спектральных каналах (для матрицы ![]() ) и дисперсиям случайных изменений компонент вектора
) и дисперсиям случайных изменений компонент вектора ![]() (для матрицы
(для матрицы ![]() ):
):
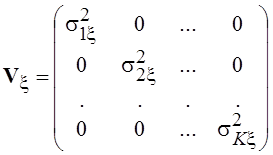 ;
; 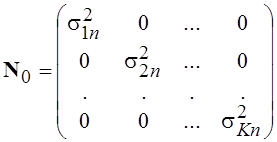 ,
,
где:
![]() - дисперсия возможных изменений концентрации j-ой газовой компоненты смеси;
- дисперсия возможных изменений концентрации j-ой газовой компоненты смеси;
![]() - дисперсия шума измерения в i-ом спектральном канале.
- дисперсия шума измерения в i-ом спектральном канале.
Примеры результатов математического моделирования показаны на рисунках 1-4, где приведены средние (по 100 измерениям) погрешности ![]() определения концентраций газов. При построении байесовской оценки для всех газов относительные среднеквадратические значения возможных изменений концентраций задавались равными 95 %, а средние значения концентраций - большими или меньшими действительных значений на 95 %.
определения концентраций газов. При построении байесовской оценки для всех газов относительные среднеквадратические значения возможных изменений концентраций задавались равными 95 %, а средние значения концентраций - большими или меньшими действительных значений на 95 %.
На рисунке 1 приведены погрешности ![]() для этилакрилата в четырехкомпонентной смеси этилен-гидразин-аммиак-этилакрилат при уменьшении концентрации этилакрилата в смеси.
для этилакрилата в четырехкомпонентной смеси этилен-гидразин-аммиак-этилакрилат при уменьшении концентрации этилакрилата в смеси.
На рисунке цифрами обозначены смеси с разными концентрациями этилакрилата: 1 – объемная концентрация этилакрилата - 5 10![]() ; 2 - 1 10
; 2 - 1 10![]() ; 3 - 2 10
; 3 - 2 10![]() ; 4 - 4 10
; 4 - 4 10![]() ; 5 - 8 10
; 5 - 8 10![]() ; 6 - 1,6 10
; 6 - 1,6 10![]() . Концентрации остальных газов в смеси постоянны и одного порядка: 1,6 10
. Концентрации остальных газов в смеси постоянны и одного порядка: 1,6 10![]() (этилен) - 3,6 10
(этилен) - 3,6 10![]() (гидразин) - 7,3 10
(гидразин) - 7,3 10![]() (аммиак) - 1,6 10
(аммиак) - 1,6 10![]() (этилакрилат). Относительное среднеквадратическое значение шума измерения σ=1%. Ряд 1 - погрешности, полученные при использовании прямого решения уравнения (4); ряд 2 – погрешности для байесовской оценки концентрации этилакрилата, найденной из (6).
(этилакрилат). Относительное среднеквадратическое значение шума измерения σ=1%. Ряд 1 - погрешности, полученные при использовании прямого решения уравнения (4); ряд 2 – погрешности для байесовской оценки концентрации этилакрилата, найденной из (6).

Рис. 1. Погрешности определения концентрации этилакрилата
Из рисунка видно, что когда концентрации газов в смеси примерно одного порядка оба метода позволяют определять концентрацию этилакрилата с небольшими погрешностями (единицы процентов). При уменьшении концентрации этилакрилата погрешности определения его концентрации возрастают для обоих методов. Однако для метода байесовской оценки погрешность возрастает гораздо медленнее и этот метод позволяет с приемлемой точностью определять концентрацию этилакрилата даже в случае, когда она на два порядка меньше концентрации других газов смеси, тогда как при использовании прямого решения уравнения (4) погрешности быстро становятся неприемлемо большими.
Погрешности определения других газов смеси являются приемлемыми для обоих методов и практически не зависят от изменения концентрации этилакрилата (см. рисунок 2, где ряд 1 и 2 – погрешности для этилена, полученные при использовании, соответственно, прямого решения уравнения (4) и байесовской оценки концентраций газов, найденной из (6); ряд 3 и 4 – соответствующие погрешности для гидразина; ряд 5 и 6 – соответствующие погрешности для аммиака; остальные обозначения те же, что на рисунке 1).
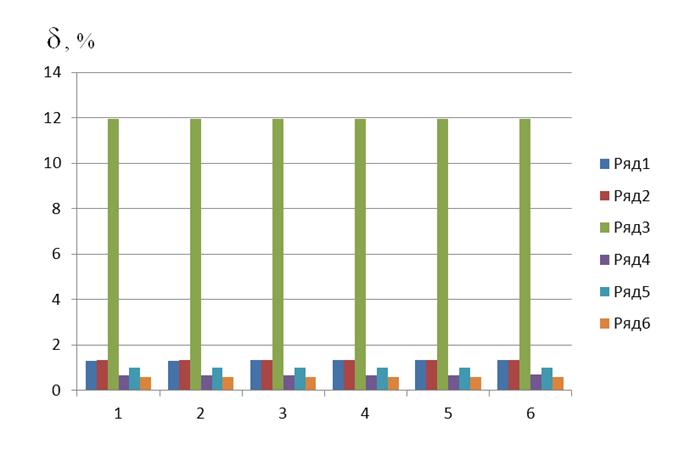
Рис. 2. Погрешности определения концентраций этилена, гидразина и аммиака
На рисунке 3 приведены погрешности ![]() определения концентрации хлоропрена в смеси этилен-хлоропрен-гидразин-аммиак в зависимости от шума измерения.
определения концентрации хлоропрена в смеси этилен-хлоропрен-гидразин-аммиак в зависимости от шума измерения.
В смеси присутствует хлоропрен, не имеющий ярко выраженных пиков поглощения в используемых спектральных каналах (измерения моделировались на линиях СО2 -лазера 10P14, 10P10, 10P20, 10P24, 10P32, 10P28, 10R6, 10R12). Концентрации газов в смеси одного порядка.
На рисунке 3: 1 – σ=4 %; 2 – 2 %; 3 – 1 %; 4 – 0,5 %; 5 – 0,25 % (другие обозначения те же, что на рисунке 1). Ряд 1 - погрешности, полученные при использовании прямого решения уравнения лазерного газоанализа (4); ряд 2 – погрешности для байесовской оценки концентраций газов, найденной из (6).
Из рисунка 3 видно, что при шуме измерения 1 % (и больше) только метод байесовской оценки позволяет определить концентрацию хлоропрена в смеси с приемлемой точностью.
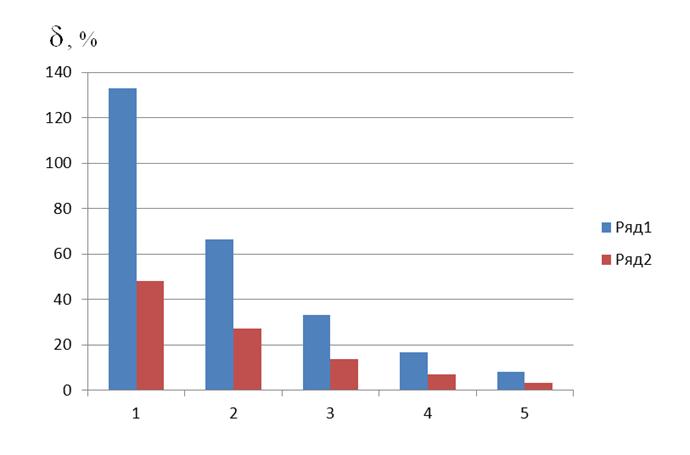
Рис. 3. Погрешности определения концентрации хлоропрена
Остальные компоненты смеси (этилен, гидразин и аммиак) имеют ярко выраженные максимумы поглощения в используемых спектральных каналах и определяются с небольшой погрешностью, которая конечно возрастает с увеличением шума измерения, но остается приемлемой (единицы процентов или по крайней мере меньше 25-30 %) при использовании обоих методов (см. рисунок 4).
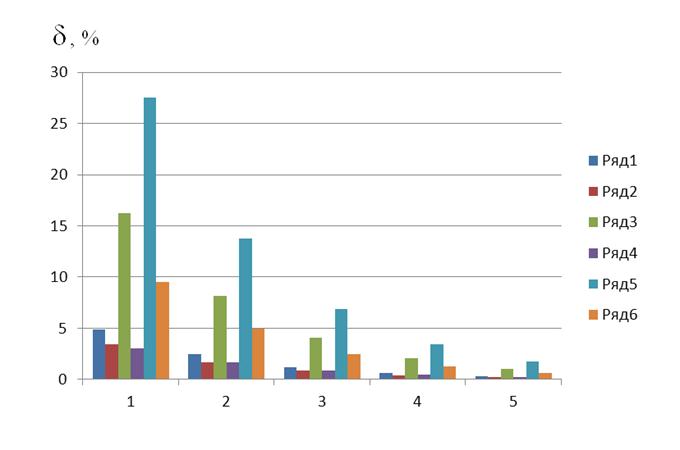
Рис. 4. Погрешности определения концентраций этилена, гидразина и аммиака
На рисунке 4: ряд 1 и 2 – погрешности для этилена, полученные при использовании, соответственно, прямого решения уравнения (4) и байесовской оценки концентраций газов, найденной из (6); ряд 3 и 4 – соответствующие погрешности для гидразина; ряд 5 и 6 – соответствующие погрешности для аммиака.
Таким образом, результаты математического моделирования показывают, что метод байесовских оценок решения уравнения лазерного газоанализа позволяет определять концентрации газов в случае сложных малокомпонентных смесей, когда концентрации компонент смеси отличаются на два порядка или компоненты газовой смеси имеют гладкий спектр поглощения без ярко выраженных максимумов поглощения, тогда как стандартный метод обработки данных измерений дает в этом случае неприемлемо большие погрешности определения концентраций газов.
Литература
1. Лазерная оптико-акустическая спектроскопия межмолекулярных взаимодействий в газах / Ю.Н. Пономарев, Б.Г. Агеев, М.В. Зигрист [и др.] Томск: МГП «РАСКО», 2000. 200 с.
2. Пономарев Ю.Н. Лазерная оптико-акустическая спектроскопия атмосферы // Оптика атмосферы и океана. 1995. Т.8. N1-2. С. 224-241.
3. Исследование причин погрешностей лазерного оптико-акустического газоанализатора / М. Зигрист, М.Ю. Катаев, А.А. Мицель, Ю.Н. Пономарев, А. Тони // Оптика атмосферы и океана. 1994, т. 7, N 11-12, с.1471-1477.
4. Лазерный оптико-акустический анализ многокомпонентных газовых смесей / В.И. Козинцев[и др.] М.: Изд-во МГТУ им. Н. Э. Баумана, 2003. 352 с.
5. Оптико-электронные системы экологического мониторинга природной среды / В.И. Козинцев, В.М. Орлов, М.Л. Белов, В.А. Городничев, Б.В. Стрелков. М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. 528 с.
6. Основы количественного лазерного анализа / В.И. Козинцев, М.Л. Белов, В.А. Городничев, Ю.В. Федотов. М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. 464 с.
7. Воскобойников Ю.Э., Преображенский Н.Г., Седельников А.Н. Математическая обработка эксперимента в молекулярной газодинамике. Новосибирск: Наука, 1984, 238 с.
8. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979, 288 с.
Публикации с ключевыми словами: лазер, газоанализ, сложные смеси, байесовская оценка
Публикации со словами: лазер, газоанализ, сложные смеси, байесовская оценка
Смотри также:
- Количественный газоанализ сложных многокомпонентных смесей
- Лазерный газоанализ многокомпонентных смесей при неточно известной матрице коэффициентов поглощения газовых компонент
- Сравнительный анализ устойчивых к выбросам сигнала методов определения количественного состава многокомпонентных газовых смесей
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (499) 263-69-71 |
|
||||
| © 2003-2024 «Инженерный вестник» Тел.: +7 (499) 263-69-71 | |||||



