электронный научно-технический журнал
ИНЖЕНЕРНЫЙ ВЕСТНИК
Издатель: Общероссийская общественная организация "Академия инженерных наук им. А.М. Прохорова".
Инженерный вестник # 07, июль 2012
УДК 004.921
Россия, МОКБ "Марс"
Россия, НИЯУ МИФИ
Россия, МГТУ им. Н.Э.Баумана
Введение
В настоящее время на рынке программного обеспечения обработки чертежей наиболее распространены три программных средства: ProcessingCenter, SheetCam и cncKad. Каждая из этих программ ориентирована на обработку чертежей под лазерную резку, и реализуют следующие функции:
- объединение отдельных дуг кривых, описывающих отверстие, в связную последовательность (а также автоматическое обнаружение и исправление незамкнутых контуров);
- работа с различными форматами чертежей (DWG, DXF и др.; ProcessingCenter работает только с указанными);
- поддержка разных станков (наиболее полный выбор предоставляет cncKad);
- задание направление обхода контуров детали;
- формирование наиболее выгодного с точки зрения времени и прочих характеристик обхода контуров (cncKad);
- учет ширину реза лазера;
- дополнительные функции для задания точного расположения чертежа на листе (поворот вокруг оси, сдвиг всего чертежа в определенную точку).
Наиболее функциональной из этих программ является cncKad. Помимо вышеперечисленного она предоставляет возможности плоскотстного (2D) и объемного (3D) моделирования, поддержку True- typeшрифтов, обеспечивает интеграцию с такими системами, как SolidWorks, SolidEdge, Autodeskи прочими, то есть по сути сочетает в себе некоторые функции САПР и обработки чертежей под конкретные условия производства.
Однако ни в одной из перечисленных программ нет функции автоматического создания точек захода на контура и тем более использовании этого для построения в некотором смысле "оптимальной" последовательности контуров для резки. А именно зачастую расположение точек захода может сыграть большую роль в итоговом выигрыше при резке. В разработанном программном средстве данная функция имеется (хотя последовательность обхода по контурам идет как на основании информации о расположении потенциальных точек, так и на основании некоторых ограничений, связанных со спецификой данного рода обработки на предприятии; таким образом, вначале рассчитывается множество возможных точек захода для контура, а уже потом только начинает формироваться последовательность обхода).
Отметим, что хотя данные средства поддерживают достаточно точные алгоритмы построения эквидистантных контуров, реализация этих алгоритмов очень сложна и не всегда используется полностью, поскольку, как уже было сказано, величина смещения достаточно мала и вполне можно обойтись приближенными алгоритмами.
В дальнейшем будут рассматриваться только плоские детали.
В настоящее время используется несколько подходов для реализации алгоритма построения эквидистанты к полилиниям. Иногда используется подход, сходный с подходом, предложенным в работе [3], а в других случаях - подходы, основанные на приближенных (с хорошей степенью точности), но при этом достаточно сложных алгоритмах, ориентированных на произвольные фигуры (см. систему AUTOCAD). Однако такие алгоритмы используются, как правило, в контексте чертежа.
Общая последовательность решения задачи:
- преобразовать все примитивы в полилинии;
- собрать все полилинии в контура – замкнутые полилинии;
- определить, какие контура являются внутренними и, соответственно, определить внешний контур (собственно, контур самой детали);
- применить алгоритм смещения к контурам;
- сформировать для каждого контура точки захода;
- сформировать последовательность обхода контуров лазером;
- задать направление обхода внешнего контура (опционально);
- перенести результат в начало глобальной системы координат (опционально).
В частности, направление смещения для полилиний вручную указывает пользователь соответствующего программного обеспечения (например, команда OFFSETв AUTOCAD: для нее нужно задать точку внутри или вне контура фигуры; отметим также тот факт, что чтобы произвести смещение контура некоторой фигуры, нужно предварительно преобразовать ее в полилинию, на что, как правило, уходит достаточно много времени, если фигура состоит из множества дуг и отрезков). При автоматической обработке электронного чертежа, отсутствует возможность непосредственно задать направление смещения для каждого конкретного контура. Таким образом, ставится задача определения направления смещения в контексте автоматизированного преобразования чертежа. Рассмотрим один из вариантов решения данной задачи.
На рисунке 1 представлен пример смещения элемента некоторого контура (пунктирной линией изображена смещенная часть; сплошной линией изображена исходная часть контура). Для каждого элемента (будь то дуга или отрезок) вычисляется два возможных варианта его смещения. Для дальнейшего построения смещенного контура необходимо выбрать только один из них, т.е. по сути определить направление смещения. Отсюда можно сделать вывод, что для каждого контура детали задача автоматического определения направления смещения (внутрь или наружу) сводится к выбору направлений смещения для каждого из сегментов этого контура.
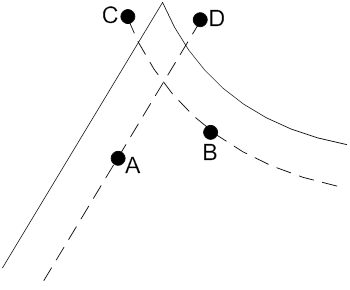
Рисунок 1. Пример определения направления смещения
Рассмотрим подробнее рисунок 1. Точки Aи B - "середины" эквидистантных сегментов (отрезка и дуги), C и D - конечные точки сегментов. Задача выбора направления смещения заключается в определении принадлежности точек A и B исходному контуру. При принятой общей последовательности решения задачи, на данном этапе уже известно, какие контура детали являются внутренними, а какой - внешним. При выборе направления смещения применяется следующее правило: если середина эквидистантного сегмента лежит внутри исходного контура, и этот контур является внутренним, то выбирается этот сегмент; если же середина эквидистантного сегмента лежит внутри исходного контура, и этот контур является внешним, то выбирается второй эквидистантный сегмент (для смещения наружу аналогично). Выбираются именно середины сегментов, поскольку величина смещения достаточно мала (и, как следствие, топология контура сохраняется). С большой степенью уверенности можно сказать, что если середина эквидистантного сегмента лежит внутри контура и смещение производится внутрь, то выбирается именного этот сегмент, поскольку все точки эквидистантного контура находятся внутри исходного (точки середин сегментов входят в это множество в силу допущений о величине смещения всех смещенных сегментов после объединения в контур; для смещения наружу аналогично). В общем случае, как при смещении внутрь, так и при смещении наружу, конечные точки сегментов (точки Cи D) могут как лежать, так и не лежать внутри исходного контура, и их нельзя использовать для определения направления смещения.
1. Алгоритм построения эквидистантного контура
После завершения работы над чертежом детали (а также вспомогательными сопроводительными документами) конструктор передает созданные документы технологу, а тот, в свою очередь, приступает к процессу ее изготовления из имеющихся материалов. Отметим, однако, что технолог непосредственно не может использовать чертеж детали для ее создания (как в случае лазерной резки, например): для этого чертеж необходимо преобразовать в некоторый формат, с которым можно было бы работать с помощью станков с ЧПУ. В настоящее время подобный "процесс преобразования" выполняется вручную, что зачастую занимает немало времени. В данной статье представлен подход, позволяющий автоматизировать большую часть функций, входящих в данный процесс преобразования.
Опишем кратко основные требования к формату представления детали, возникающие при использовании лазерных станков.
1) У каждого контура детали (как у внутренних, так и у внешнего) должны быть определены точки захода (подробное описание этого понятия см. ниже).
2) Важен порядок обхода контуров детали: сначала лазером должны быть вырезаны внутренние контура, а последним должен быть вырезан внешний контур; также, возможно, стоит задать определенное направление обхода (по и против часовой стрелки).
3) Должна быть сделана поправка на ширину реза лазера (англ. «offset»-смещение). При этом величина смещения в общем случае зависит от толщины и вида исходного материала (подробное описание см. ниже).
Определим понятие точки захода. Точка захода – точка, с которой лазер начинает вырезать данный контур. Эта точка должна быть первая в последовательности всех точек контура, причем вторая и последняя точки из этой последовательности фактически совпадают (так как контур представляет собой замкнутую кривую). Очевидно, что расположение данных точек захода зависит от того, является ли данный контур внешним или внутренним: в случае, если контур внутренний, точка захода должна находиться внутри контура, а в случае внешнего контура – снаружи него. При этом желательно, чтобы переход от точки захода к точке контура был максимально плавным, т.е. в самом лучшем случае линия, соединяющая точку захода и точку контура была продолжением линии, соединяющей следующие две точки (рисунок 2).
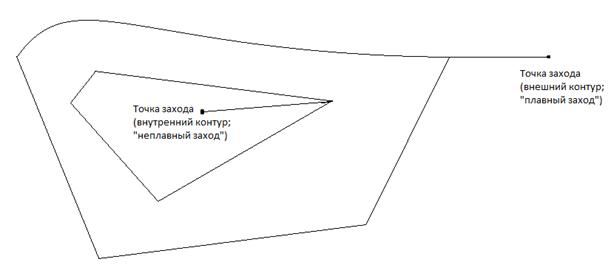
Рисунок 2. Пример точек захода для внешнего и внутреннего контуров детали
Эквидистантный контур необходимо построить для того, чтобы учесть ширину реза лазера. Отметим, что смещение для внутренних контуров должно быть сделано «внутрь», а для внешнего контура – «наружу». Пример смещения для контуров детали (внутреннего и внешнего) представлен на рисунке 3.

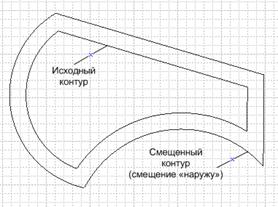
Рисунок 3. Пример смещения для внутреннего и для внешнего контуров
Величина смещения обычно находится в пределах от 0,1 до 0,5 мм, т.е. является достаточно малой, и это позволяет сделать допущение о том, что исходный и эквидистантный контур имеют одинаковую топологию (как на рисунке 3). В дальнейшем будем полагать, что операция смещения контура не "меняет" его геометрию (то есть рассматриваются ситуации, подобные тем, что изображены на рисунке 3).
Будем полагать, что. чертеж детали выполнен в масштабе 1:1, не содержит габаритных размеров детали (рисунок 4), а также контура детали не содержат пересекающихся/перекрещивающихся отрезков. Тогда схематически процесс преобразования чертежа может быть представлен в виде, изображенном на рисунке 4:
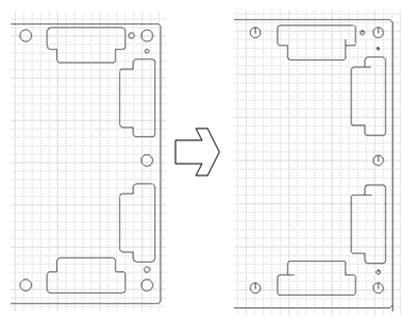
Рисунок 4. Пример преобразования чертежа
Будем называть полученный после преобразования чертеж чертежом-траекторией.
Без ограничения общности будем полагать, что чертеж детали - файл формата DXF [1].
Отметим, что задачи преобразования всех примитивов в полилинии (1), а также сборка полилиний в контура (2) решаются достаточно просто. Чтобы дугу преобразовать в полилинию, достаточно рассчитать ее кривизну и конечные точки [1]. Чтобы преобразовать окружность в полилинию, достаточно разбить ее на несколько дуг и применить описанное выше решение для дуг. Линии тривиально преобразуются в полилинии из двух точек.
Задача сборки полилиний в контура (3) сводится к последовательному перебору всех полилиний и соединению их конечных точек по принципу равенства координат.
Для решения задачи определения внешнего контура детали можно предложить два варианта решения: приближенный метод ограничений (каждый контур ограничивается прямоугольником. Таким образом, задача определения внешнего контура сводится к задаче определения точки внутри прямоугольника и с известными координатами его вершин) и более точный - с использованием алгоритма определения нахождения точки внутри контура (когда все заданные граничные точки одного контура проверяются на нахождение внутри другого контура) [2].
Реализация операции смещения контуров является наиболее сложной и громоздкой, поэтому остановимся на ней более подробно.
Положим, что контур состоит из комбинации следующих графических элементов (примитивов): линия (отрезок или линейный сегмент), дуга (дуговой сегмент). Окружность можно рассматривать, как комбинацию четырех дуг (как было описано выше). Таким образом получаем, что всего возможны четыре комбинации примитивов: линия и линия, линия и дуга, дуга и линия, дуга и дуга. Положим, что offsetPolyline - формируемая полилиния ("смещенный контур").
1.1 Случай двух линейных сегментов
Рассматриваемая ситуация изображена на рисунке 5.
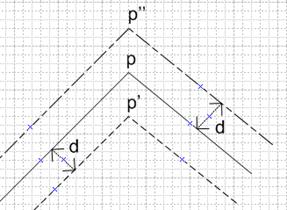
Рисунок 5. Случай двух линейных сегментов
Данный случай является самым простым из всех четырех. На рисунке введены следующие обозначения: p – точка пересечения линейных сегментов исходного контура, p' – точка пересечения смещенных сегментов в случае, когда смещение идет «вниз» по отношению к точке p, p'' - точка пересечения смещенных сегментов в случае, когда смещение идет «вверх» по отношению к точке p, d – величина смещения. Заметим, что в данной ситуации невозможно определить, для какого контура реализуется смещение – для внешнего или для внутреннего контура детали (точка p'' необязательно точка смещенного внешнего контура, а p' необязательно точка смещенного внутреннего контура; такая ситуация справедливая и для других комбинаций примитивов). Эта задача решается с помощью алгоритма определения нахождения точки внутри контура [2], а также знания о контуре (на этом шаге известно какой контур - внутренний или внешний, соответственно смещение рассчитывается внутрь или наружу контура).
Прежде, чем искать координаты точки p' (p''), необходимо сначала получить смещенные линейные сегменты для каждого из двух исходных линейных сегментов. Найдя их, мы сможем найти точку p' (p'') как точку пересечения этих смещенных сегментов (или их продолжений).
Рассмотрим ситуацию, изображенную на рисунке 6. Положим, что AB – исходный линейный сегмент, для которого необходимо найти смещенный «аналог»; AC, AD, AB – вектора. Рассмотрим общий случай смещения сегмента в обе стороны (в направлении AD и AC). Положим, что длина векторов AD, AC равна d – величине смещения.
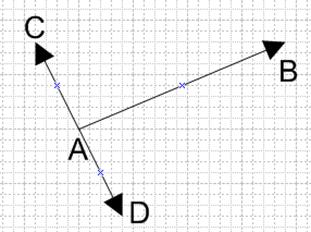
Рисунок 6. К реализации смещения в случае двух линейных сегментов
Очевидно, что смещенные линейные сегменты параллельны исходному (и как следствие, параллельны друг другу), то есть точки C и D – «смещенная» точка A в оба направления. При этом вектора AC и AD перпендикулярны вектору AB, т.е. их скалярное произведение равно 0. Таким образом, можно выделить соотношения
![]() (AB,AC)=0; |AC|=d.
(AB,AC)=0; |AC|=d.
Эти соотношения можно представить в виде системы уравнений
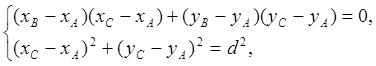
где ![]() ,
,![]() - координаты точки А;
- координаты точки А; ![]() ,
,![]() - координаты точки B;
- координаты точки B; ![]() ,
,![]() - координаты точки C. При этом координаты точки C являются неизвестными. Данная система будет иметь два решения: координаты точки C и координаты точки D. После нахождения решения аналогичные действия проводятся с точкой B (чтобы получить другой конец смещенной линии). В результате получим координаты четырех точек, две из которых соответствуют одной смещенной линии, а две оставшихся – другой.
- координаты точки C. При этом координаты точки C являются неизвестными. Данная система будет иметь два решения: координаты точки C и координаты точки D. После нахождения решения аналогичные действия проводятся с точкой B (чтобы получить другой конец смещенной линии). В результате получим координаты четырех точек, две из которых соответствуют одной смещенной линии, а две оставшихся – другой.
Отметим, что поскольку через две точки можно провести только одну прямую, мы можем вычислить уравнение этой прямой. Как известно из аналитической геометрии, уравнение прямой имеет вид: Ax+By+C=0. Зная координаты двух точек (обозначим их 1 и 2), мы можем найти значения коэффициентов A, B и C из системы уравнений
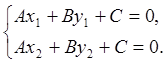
В рассматриваемой ситуации данная система уравнений всегда будет иметь единственное решение (точка 1 и точка 2 не совпадают).
Проделав описанную выше процедуру для каждого линейного сегмента и определив, какие смещенные сегменты необходимо выбрать, можно найти координаты их точки пересечения (а это возможно сделать, т.к. все необходимые коэффициенты на данном этапе уже найдены). После того, как точка пересечения найдена, она добавляется в offsetPolyline (ее параметр bulge полагается равным 0).
1.2 Случай линейного сегмента и дугового сегмента
Рассматриваемая ситуация изображена на рисунке 7.
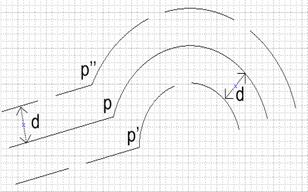
Рисунок 7. Случай линейного сегмента и дуги
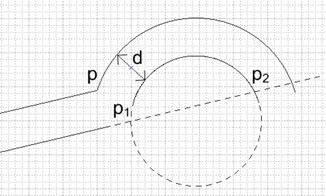
Рисунок 8. Получение смещения в случае линейного и дугового сегментов
Как и в предыдущем случае для получения результирующей точки (p' или p''), которая потом будет добавлена в offsetPolyline, необходимо сместить сначала оба сегмента, а затем найти точку их пересечения (или точку пересечения их продолжений). Отметим, что задача смещения дуги сводится к уменьшению/увеличению ее радиуса на величину смещения.
В общем случае имеется не более двух точек пересечения (p1 и p2) линейного сегмента и дуги (случаи, когда пересечения нет или оно одно рассмотрены ниже). Координаты этих точек можно найти из системы уравнений
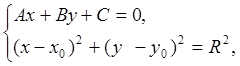
где A,B,C– коэффициенты уравнения прямой, на которой лежит смещенный линейный сегмент; x0, y0 – координаты центра дуги; R – радиус смещенной дуги (поправка исходного радиуса на величину смещения).
1.2.1 Система имеет два решения
В данном случае имеет место ситуация, изображенная на рисунке 8. При этом ставится вопрос: какую же точку из двух выбрать? Из двух полученных точек выбирается ближайшая точка к точке p. Как видно из рисунка, этой точкой является точка p1. Она добавляется в offsetPolyline и при этом ее параметр bulge[1] устанавливается в 0 (т.к. в дальнейшем, когда мы перейдем к следующей точке исходного контура, которая в свою очередь будет являться концом дуги, у нас уже будет информация об угле раствора смещенной дуги и соответственно мы сможем вычислить данный параметр).
1.2.2 Система имеет одно решение
Тут возможны две ситуации:
a) конечная точка смещенной дуги совпадает с конечной точкой смещенного линейного сегмента (при этом продолжения сегментов не участвуют в пересечении);
b) происходит касание продолжения смещенного линейного сегмента и окружности, содержащей смещенную дугу.
Рассмотрим вторую ситуацию (рисунок 9).
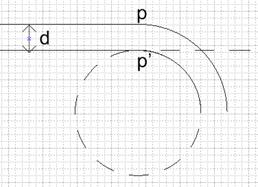
Рисунок 9. К ситуации a)
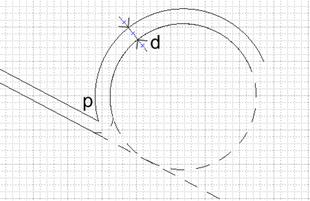
Рисунок 10. К ситуации b)
Отличие данной ситуации от той, что описана в п.1. состоит только в количестве точек пересечения – в данном случае она одна. Соответственно ее и добавляем к offsetPolyline.
В случае ситуации b (рисунок 10) возникает необходимость добавить «скругление». Данная ситуация не рассматривается в силу сказанных выше допущений об "изменении" топологии контура.
1.2.3 Система не имеет решений
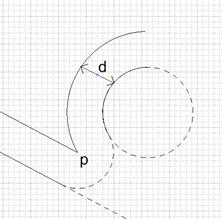
Рисунок 11. К случаю 1.2.3
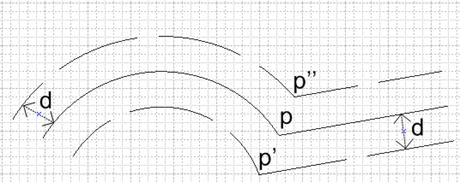
Рисунок 12. Случай дугового и линейного сегментов.
Данная ситуация не рассматривается аналогично ситуации b для случая 1.2.2.
1.2.4 Случай дугового сегмента и линейного сегмента
Рассматриваемая ситуация изображена на рисунке 12. Ситуация в принципе аналогична предыдущей, однако в данном случае стоит задача вычисления параметра bulge для начальной точки смещенной дуги. В данном случае сначала выполняются действия, описанные в предыдущем пункте (вычисляется смещение каждого сегмента отдельно, затем находится общее смещение, т.е. точка p' (p'')). После этого идет вычисление собственно параметра bulge начальной точки смещенного дугового сегмента (на основе информации о центре смещенной дуги, начальной точке, полученной на предыдущем шаге алгоритма, а также на основе информации о конечной точке, вычисленной на данном шаге). После этого значение параметра bulge сохраняется, а в offsetPolyline добавляется полученная точка, у которой bulge устанавливается в 0 (т.к. после нее идет линейный сегмент).
1.2.5 Случай двух дуговых сегментов
Теперь рассмотрим оставшийся случай идущих подряд двух дуговых сегментов (рисунок 13).
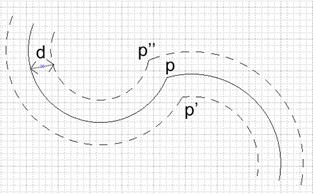
Рисунок 13. Случай двух дуг
Подход в данном случае схож с описанным выше. Точно также строятся смещенные дуги, происходит их «склеивание» с предыдущими точками (корректировка параметра bulge). Отличие состоит в том, что для поиска точки p' (p'') необходимо решить систему уравнений
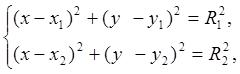
где x1,y1 – координаты центра первой смещенной дуги, x2,y2 – координаты центра второй эквидистантной дуги, R1 – радиус первой эквидистантной дуги, R2 – радиус второй эквидистантной дуги. При решении данной системы возможны ситуации, представленные ниже.
1) Система имеет два решения
Самая распространенная ситуация: две точки пересечения. Из них выбирается ближайшая точка к p (на рис. 14 это точка p1), которая затем добавляется в offsetPolyline (значение параметра bulge для нее будет вычислено на следующем шаге алгоритма, как в предыдущих описанных случаях).
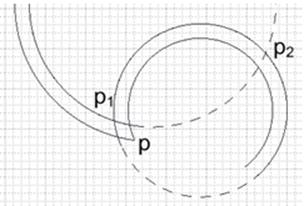
Рисунок 14. К ситуации 1
2) Система имеет одно решение
Тут возможны две ситуации
2.1) Конечная точка первой смещенной дуги совпадает с начальной точкой второй смещенной дуги (при этом продолжения сегментов не участвуют в пересечении, т.е. имеет место касание смещенных дуг).
Данная ситуация изображена на рисунке 15.
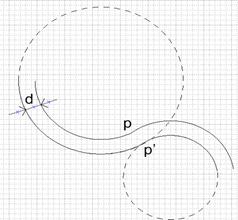
Рисунок 15. К ситуации 2.1
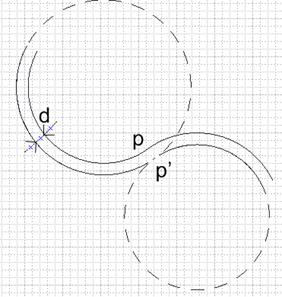
Рисунок 16. К ситуации 2.2
В этом случае в offsetPolyline добавляется данная точка касания окружностей p' (значение параметра bulge для нее будет вычислено на следующем шаге алгоритма, как в предыдущих описанных случаях).
2.2) Касание продолжений смещенных сегментов (касание окружностей)
Данная ситуация не рассматривается в силу сказанных выше допущений (комментарии к рисунку 3).
3) Система не имеет решений
В этом случае имеет место ситуация, изображенная на рисунке 17.
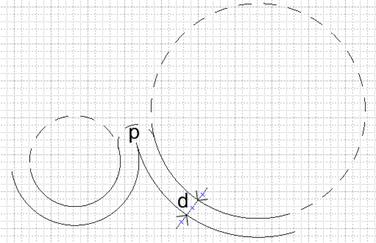
Рисунок 17. К ситуации 3
Данная ситуация не рассматривается согласно предположению о геометрии контура.
В результате прохода по всем точкам, offsetPolyline содержит все точки смещенного контура. Такая процедура проделывается для каждого контура (с учетом, естественно, того, является ли этот контур внешним или внутренним). Отметим, что на данном шаге также необходимо вычислить параметр bulgeдля предыдущей точки контура.
Процесс формирования точек захода основан на последовательном проходе по всем точкам контура и расчете для каждой из них вероятной точки захода (как «плавной», так и «неплавной»). Стоит отметить, что в случае формировании точки захода для внешнего контура конечной целью алгоритма является нахождение точки захода, максимально близкой к какому-либо из концов внешнего контура детали, а в случае внутреннего контура - просто формирование всех возможных. При этом, если есть возможность построения как "плавного захода", так и "неплавного" (рисунок 1), предпочтение отдается "плавному". Построение "плавного" захода заключается в построении отрезка, лежащего на продолжении другого отрезка, соединяющего две точки контура. "Неплавный заход" может быть построен любым доступным способом Это формируемое множество точек захода будет использовано при построении последовательности контуров, в которой будет двигаться лазер.
Задача формирования последовательности контуров таким образом, чтобы холостые проходы лазерной головки были сведены к минимуму (то есть задача получения некоторого «оптимального обхода» контуров детали) является в общем случае чрезвычайно сложной, т.к. каждая деталь имеет в общем случае абсолютно различную структуру. В случае, если производство в некотором приближении можно считать серийным, задача реализации данного алгоритма значительно упрощается.
1) Задать направление обхода внешнего контура
Для определения того, в каком направлении обходится построенный контур, можно применить метод определения знака площади контура. Суть его состоит в переборе всех точек контура, на каждом шаге вычисляется площадь прямоугольной трапеции, образованной отрезком границы контура, ее проекцией на ось абсцисс, а также перпендикулярами к ней, опущенными из точек этого отрезка. Полученная величина прибавляется к уже вычисленной, причем площадь берется с знаком "+", если величина проекции больше 0 и "-" в противном случае. Если знак суммарной полученной площади больше 0, то обход отверстия идет по часовой стрелке, если меньше 0 - против часовой стрелки. Если необходимо поменять направление обхода контура, то достаточно просто инвертировать последовательность его точек (отметим тот факт, что контур может содержать дуги; площадь в этом случае рассчитывается также, только предварительно дугу надо разбить на некоторое количество отрезков)
2) Перенести результат в начало глобальной системы координат
Данная операция делается с помощью параллельного переноса.
Заключение
Таким образом, задачу преобразования чертежа в чертеж-траекторию в некотором подмножестве множества всех чертежей можно считать решенной. Стоит отметить, что хотя данный алгоритм ограничен по возможностям, он охватывает достаточно широкий спектр возможных чертежей, и может быть использован на большом множестве различных вариантов чертежей деталей.
Литература
1. http://usa.autodesk.com/adsk/servlet/item?linkID=10809853&id=12272454&siteID=123112
2. http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
3. Xu-Zheng Liu, Jun-Hai Yong, Guo-Qin Zheng, Jia-Guang Sun. An offset algorithm for polyline curves. Computers in Industry 58 (2007) 240–254
Публикации с ключевыми словами: лазерная резка, полилиния, эквидистанта, точка захода
Публикации со словами: лазерная резка, полилиния, эквидистанта, точка захода
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (499) 263-69-71 |
|
||||
| © 2003-2024 «Инженерный вестник» Тел.: +7 (499) 263-69-71 | |||||



