электронный научно-технический журнал
ИНЖЕНЕРНЫЙ ВЕСТНИК
Издатель: Общероссийская общественная организация "Академия инженерных наук им. А.М. Прохорова".
Инженерный вестник # 05, май 2012
УДК 517.97
Россия, МГТУ им. Н.Э. Баумана
Введение
Составление карт местности является одной из центральных задач современной картографии. Для её решения часто используют аэрофотосъёмку с применением самолёта, который облетает на определенной высоте соответствующую местность с её фотографированием. В этом случае одна из аэронавигационных задач состоит в определении типа зависимости замкнутой траектории облета местности, начинающейся из начальной точки, при которой она охватывает максимальную площадь ![]() при заданных боковой нечёткой скорости ветра
при заданных боковой нечёткой скорости ветра ![]() и чёткой курсовой скорости
и чёткой курсовой скорости ![]() самолёта.
самолёта.
При ![]() в научной литературе эта задача известная как задача финикийской царевны Дидоны о выборе типа линии фиксированной длины, окружающей максимально возможную площадь (изопериметрическая задача), которая решается типовыми методами вариационного исчисления [1, 2].
в научной литературе эта задача известная как задача финикийской царевны Дидоны о выборе типа линии фиксированной длины, окружающей максимально возможную площадь (изопериметрическая задача), которая решается типовыми методами вариационного исчисления [1, 2].
Модификация этой изопериметрической задачи при![]() известна как задача Чаплыгина и она решается так же методами вариационного исчисления [3].
известна как задача Чаплыгина и она решается так же методами вариационного исчисления [3].
Ниже решается простейший вариант нечёткой задачи Чаплыгина, когда скорость ветра ![]() задается в виде нечеткого числа
задается в виде нечеткого числа ![]() с треугольной функцией принадлежности, которая характеризует вариацию скорости ветра в процессе облёта заданной области. Это представляет научную новизну сформулированной выше задачи.
с треугольной функцией принадлежности, которая характеризует вариацию скорости ветра в процессе облёта заданной области. Это представляет научную новизну сформулированной выше задачи.
Постановка задачи
Формализуем нечёткую задачу Чаплыгина. Для этого введём декартову систему координат ![]() в горизонтальной плоскости относительно Земли, проходящей через замкнутый плоский контур
в горизонтальной плоскости относительно Земли, проходящей через замкнутый плоский контур ![]() , по которому происходит облёт самолетом области
, по которому происходит облёт самолетом области ![]() площадью
площадью ![]() (рис. 1). Найдем тип оптимизируемого функционала.
(рис. 1). Найдем тип оптимизируемого функционала.
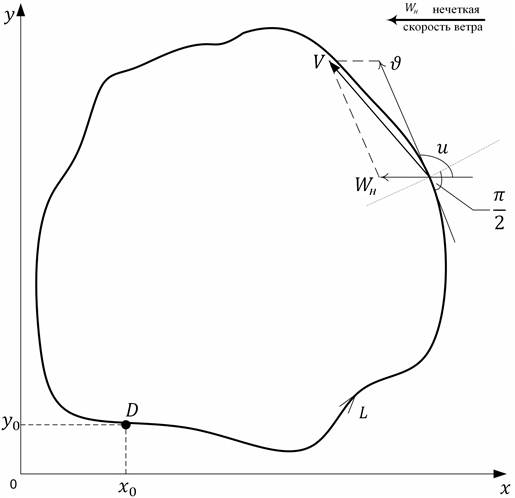
Рис. 1. Проекция на горизонтальную плоскость траектории L облёта самолетом области D.V-курсовая скорость; ![]() - путевая скорость; Wн - нечёткая скорость ветра
- путевая скорость; Wн - нечёткая скорость ветра
Контур ![]() в параметрической форме имеет вид
в параметрической форме имеет вид ![]() поэтому формула Грина при
поэтому формула Грина при ![]() для односвязной области
для односвязной области ![]() которая ограничена замкнутым контуром
которая ограничена замкнутым контуром ![]() будет иметь вид:
будет иметь вид:
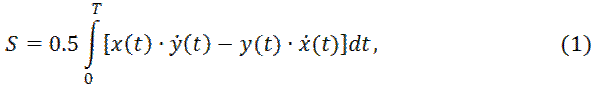
где ![]() заданное время облёта области
заданное время облёта области ![]() по траектории
по траектории ![]()
На функционал (1) наложим ограничения (рис.1):
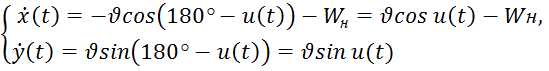 (2)
(2)
с чёткими краевыми условиями:
![]() (3)
(3)
Задача ![]() состоит в выборе такого управления
состоит в выборе такого управления ![]() [10, 11], при котором, начав движение из чёткой точки
[10, 11], при котором, начав движение из чёткой точки ![]() (3), самолёт облетит за заданное чёткое время
(3), самолёт облетит за заданное чёткое время ![]() область
область ![]() максимальной нечёткой площади
максимальной нечёткой площади ![]() при ограничениях (2) с нечёткой величиной
при ограничениях (2) с нечёткой величиной ![]() с треугольной функцией принадлежности
с треугольной функцией принадлежности ![]()
При чётком условии ![]() в (2) соответствующую задачу принято называть задачей Чаплыгина [5, 6]. При нечётком условии
в (2) соответствующую задачу принято называть задачей Чаплыгина [5, 6]. При нечётком условии ![]() задачу
задачу ![]() будем называть нечёткой задачей Чаплыгина, которая является естественным обобщением её четкого аналога. В
будем называть нечёткой задачей Чаплыгина, которая является естественным обобщением её четкого аналога. В ![]() нечёткость интерпретируется как вариация скорости ветра.
нечёткость интерпретируется как вариация скорости ветра.
Задача ![]() является нечёткой вариационной задачей Лагранжа без ограничений на управление [9]. В соответствии с постановкой задачи необходимо найти оптимальную траекторию и оптимальное нечёткое значение площади
является нечёткой вариационной задачей Лагранжа без ограничений на управление [9]. В соответствии с постановкой задачи необходимо найти оптимальную траекторию и оптимальное нечёткое значение площади ![]() облета области
облета области ![]() .
.
Метод решения
Для решения задачи ![]() используем принцип максимума [5, 6].
используем принцип максимума [5, 6].
Гамильтониан ![]() имеет вид
имеет вид
![]()
где ![]() вспомогательные переменные.
вспомогательные переменные.
Находим максимум ![]() по управлению:
по управлению:
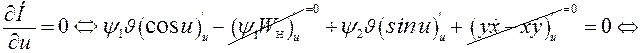
![]()
Сопряженные уравнения определяются системой
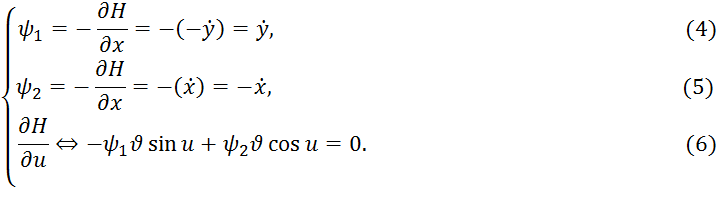
Из (4) имеем![]() а из (5) соответственно
а из (5) соответственно![]()
После подстановки этих значений в (6), преобразований и переобозначений получим
(![]()
Введем замену переменных:
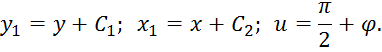
Тогда (2), (7) будут иметь вид
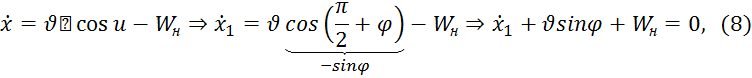
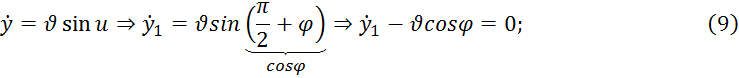
(![]()
![]() ⇒
⇒ ![]() (10)
(10)
Из (10) следует, что:

Кроме того имеем
![]()
![]()
Полученные соотношения (8) – (11) определяют кривую второго порядка в полярной системе координат ![]()
Действительно из (11) имеем:
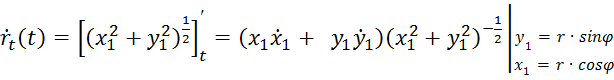 =
=
= 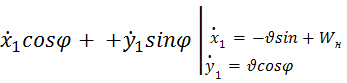 =
=
= ![]()
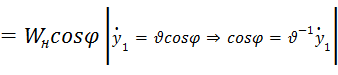 =
=![]()
Таким образом, получим
![]()
откуда после интегрирования будем иметь
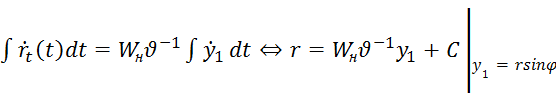 ⇒
⇒
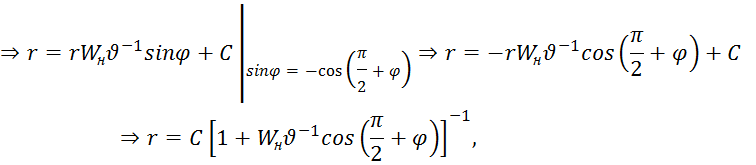
![]()
Таким образом, при ![]() получим полярное уравнение нечёткого эллипса, где
получим полярное уравнение нечёткого эллипса, где ![]() – нечёткий эксцентриситет,
– нечёткий эксцентриситет, ![]() - фокальный параметр (рис. 2):
- фокальный параметр (рис. 2):
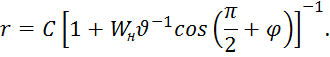

Рис. 2. Оптимальная траектория (эллипс) Lоблёта самолётом максимальной площадью Sпри наличии нечёткой скорости ветра Wн
Нечёткая площадь ![]() полученного эллипса[7]
полученного эллипса[7]
![]()
где![]() большая полуось нечёткого эллипса;
большая полуось нечёткого эллипса;![]() малая полуось;
малая полуось;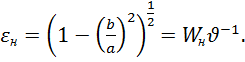
Определим параметры эллипса ![]() , используя заданное время
, используя заданное время ![]() Элемент дуги
Элемент дуги ![]() кривой, заданной в явной форме
кривой, заданной в явной форме ![]() самолёт пролетает за элемент времени
самолёт пролетает за элемент времени ![]() с курсовой скоростью
с курсовой скоростью ![]() :
:
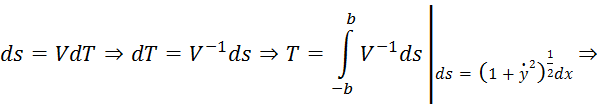

По теоремы косинусов имеем (рис.2):
![]()
Кроме этого:
![]()
Выразим![]() через
через ![]() из квадратного относительно
из квадратного относительно![]() уравнения:
уравнения:
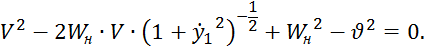
Тогда после преобразований получим выражение
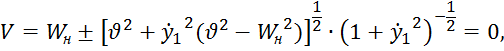
которое после подстановки в (12) и преобразований даёт
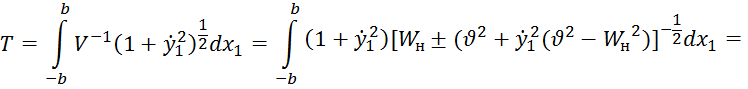
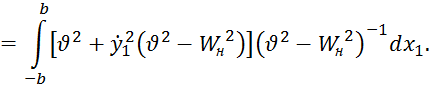
Отсюда имеем
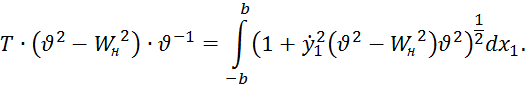
Обозначеним
![]()
Тогда последнее выражение будет приобретает вид:
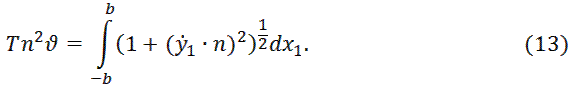
Из канонического уравнения эллипса в координатах ![]() имеем (рис.2):
имеем (рис.2):
![]()
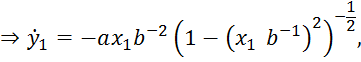
которые после подстановки его в (13) и интегрирования даёт
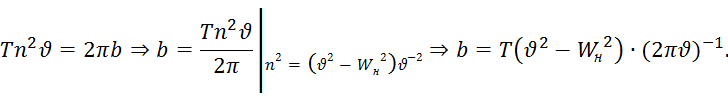
Отсюда
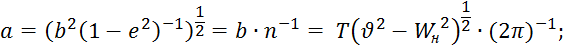
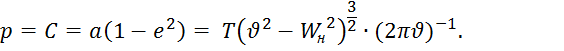
В результате получим
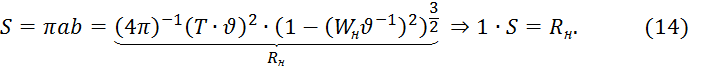
Пусть![]() тогда нечёткое
тогда нечёткое ![]() находится из расширенной нечёткой линейной системы (НЛС) [8]:
находится из расширенной нечёткой линейной системы (НЛС) [8]:
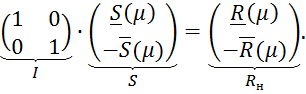
Поэтому имеем:
![]() =
=![]() .
.
Здесь![]() ,
,![]() зависят от
зависят от![]() , поэтому возможны «сильное» или «слабое» решения расширенной НЛС.
, поэтому возможны «сильное» или «слабое» решения расширенной НЛС.
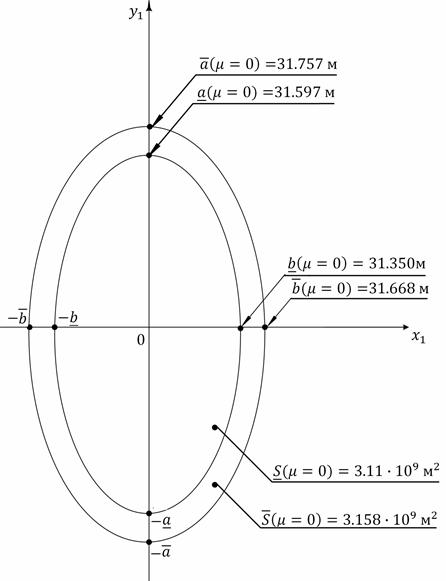
4. Числовой пример.
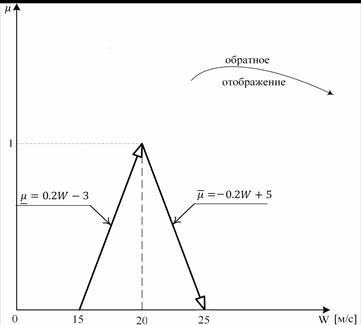
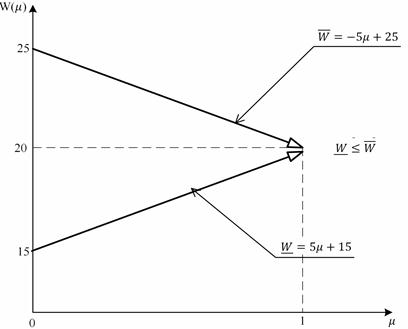
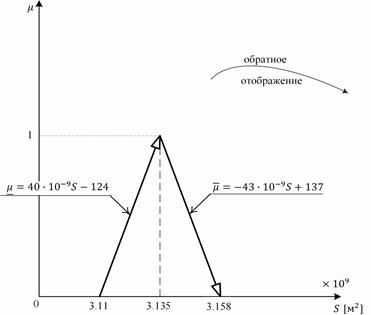
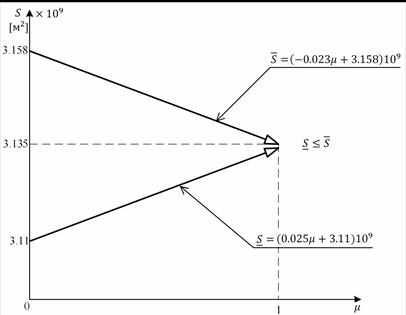
Пусть имеем (рис. 3а-3в):
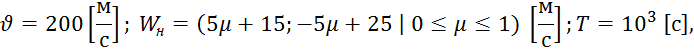
тогда из (14) получим, что ![]() не является нечётким числом, т.к.
не является нечётким числом, т.к. ![]() возрастает, а
возрастает, а![]() убывает, поэтому после соответствующей замены получим «слабое» решение нечёткой задачи Чаплыгина.
убывает, поэтому после соответствующей замены получим «слабое» решение нечёткой задачи Чаплыгина.
|
|
Рис. 3а. Нечёткая скорость | |
|
|
Рис. 3б. Нечёткая площадь
| |
| |
Рис.3в. Нечёткая траектория (эллипс) | |
 ≃
≃
≃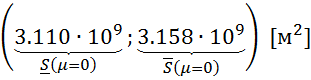 .
.
Нечёткие параметры эллипса будут соответственно равны
 ≃(31.350; 31.668) [м];
≃(31.350; 31.668) [м];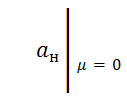 ≃(31.597; 31.757) [м].
≃(31.597; 31.757) [м].
Таким образом, для заданных исходных данных нечёткий эллипс незначительно отличается от нечёткой окружности.
Выводы
Решена задача по нахождению оптимальной траектории облёта самолетом области при воздействии на самолёт нечёткой боковой скорости ветра.
С использованием принципа максимум для решения нечёткой вариационной задачи получено «слабое» решение относительно площади облёта самолетом.
6. Заключение.
Выше решалась задача по нахождению оптимальной траектории облёта самолётом области при нечёткой величине скорости бокового ветра и чёткой курсовой скорости самолёта. Подобным способом может быть решена задача при наличии нечётких курсовой скорости самолёта и боковой скорости ветра.
Литература.
1. Пантелеев А.В. Вариационное исчисление в примерах и задачах. М., Высшая школа, 2006.
2. Панов В.Ф. Математика древняя и юная. М., МГТУ им.Н.Э.Баумана, 2006.
3. Ченцов Н.Г. О траектории аэроплана, охватывающей наибольшую плоскость. Вестник воздушного флота №1,2, 1925, с.469-473.
4. Гаврилов В.Р. и др. Кратные и криволинейные интегралы. Элементы теории поля. М., МГТУ им.Н.Э.Баумана, 2008.
5. Брайсон А.,Хо Ю-Ши. Прикладная теория оптимального управления. М., Мир, 1972.
6. Афанасьев В.Н. и др. Математическая теория конструирования систем управления. М., Высшая школа, 2008.
7. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М., МГТУ им.Н.Э. Баумана, 2005.
8. Menahem Friedman. Fuzzy linear systems. Fuzzy sets and systems, 96(1998), 201-209
9. Мочалов И.А. и др. Методы робастного, нейро-нечеткого и адаптивного управления. М., МГТУ им. Н.Э. Баумана, 2001.
10. Мочалов И.А. Нечеткие вероятностно-статистические методы в задачах управления. Гл. 9-11. М., Электронный носитель на CD, МГТУ им. Н.Э. Баумана, 2003.
11. Мочалов И.А. Методические материалы по нечетким методам в задачах управления. М., Электронный носитель на CD, МГТУ им. Н.Э. Баумана, 2004
Публикации с ключевыми словами: Чаплыгин, нечёткий эллипс, слабое решение, курсовая скорость
Публикации со словами: Чаплыгин, нечёткий эллипс, слабое решение, курсовая скорость
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (499) 263-69-71 |
|
||||
| © 2003-2024 «Инженерный вестник» Тел.: +7 (499) 263-69-71 | |||||